2022-10-05

競技プログラミングでも出題されそうな数学オリンピックの問題

この記事では、数学オリンピックで出題された問題を競技プログラミングの形式に変換して紹介します（変換とは言ったものの、制約以外一切改変なしです）。実行時間とメモリの制限は2秒、1024MB程度を想定しています。

問題

$N$ 頂点 $M$ 辺の連結な単純無向グラフが与えられます。頂点には $1, 2, \ldots, N$ の番号が、辺には $1, 2, \ldots, M$ の番号が振られており、辺 $i$ は頂点 $U_i$ と $V_i$ を結びます。数列 $A_1, A_2, \ldots, A_N$ と $B_1, B_2, \ldots, B_M$ であって、次の条件を満たすものを $1$ つ構築してください。

$A_i$ は $1$ または $2$
$B_i$ は $1$ または $2$ または $3$
頂点 $v$ に対して $S_v$ を $\displaystyle S_v = A_v + Σ_{頂点vは辺iの端点である} B_i$ 　で定める。 $2$ つの頂点 $v$ と $w$ が隣接するとき、 $S_v \neq S_w$ である。

（出典：Baltic Way 2020 Problem 9　Baltic Way 2020 – virtual competition）

制約

$2 \leq N \leq 10^5$
$1 \leq M \leq 10^5$
$1 \leq U_i \leq N$
$1 \leq V_i \leq N$
与えられるグラフは連結な単純グラフである。

解説

クリックで解説を見る

クリックで実装例を見る（C++）

#include <bits/stdc++.h>
using namespace std;

typedef pair<int,int> iint;

// output
template<class T> ostream& operator<<(ostream &ostr, const vector<T> &vec){
    int N = vec.size();
    if(N == 0) return ostr;
    ostr << vec[0];
    for (int i = 1; i < N; i++) {
        ostr << " " << vec[i];
    }
    return ostr;
}

int main(){
    int N, M;
    cin >> N >> M;
    vector<vector<int>> G(N);
    map<iint, int> mp;
    for (int i = 0; i < M; i++) {
        int u, v;
        cin >> u >> v;
        u--; v--;
        if(u > v) swap(u, v);
        G[v].push_back(u); // indexの大きい頂点からのみ参照
        mp[{u, v}] = i; // 辺番号
    }

    vector<int> A(N, 1); // A_i
    vector<int> B(M, 2); // B_i
    vector<int> S(N, 1); // S_i
    for (int i = 0; i < N; i++) {
        for (int v : G[i]){
            S[i] += 2;
            S[v] += 2;
        }
    }

    for (int i = 0; i < N; i++) {
        int si = S[i];
        int mins = si; // S_i を区間[mins, maxs]の整数から選べる
        int maxs = si;
        int k = G[i].size();
        set<int> s;

        for (int j = 0; j < k; j++) {
            if(A[G[i][j]] == 1){
                mins--;
            }
            else{
                maxs++;
            }
            s.insert(S[G[i][j]]);
        }   

        int news; // S_i を newsに変更する
        for (int j = mins; j <= maxs; j++) {
            if(!s.count(j)){
                news = j;
                break;
            }
        }
        for (int j = 0; j < k; j++) {
            if(A[G[i][j]] == 1){
                if(news < S[i]){
                    A[G[i][j]] = 2;
                    B[mp[{G[i][j], i}]] = 1;
                    S[i]--;
                }
            }
            else{
                if(news > S[i]){
                    A[G[i][j]] = 1;
                    B[mp[{G[i][j], i}]] = 3;
                    S[i]++;
                }
            }
        }   
    }

    cout << A << endl;
    cout << B << endl;
}

2019-12-29

【ペア作りシリーズ②】ジジ抜きが可能なのはいつか

ペア作りシリーズ数学

0.ごあんない
1.「任意2人組作り可能」を別の意味に解釈する
2.非連結の場合
3.連結グラフに関する考察の方針
4.連結の場合
5.結論
6.今後の展望

0.ごあんない

この記事は「ペア作りシリーズ」の2本目の記事となります。
1本目の記事のリンクはこちらです。一応、1本目を読んでいなくてもわかるようにはなっていると思いますが、ぜひ1本目もお読みください。

mel9.hatenadiary.com

1.「任意2人組作り可能」を別の意味に解釈する

1.1.神経衰弱可能

前の記事では、どのような順番で2人組を作っても、全員があぶれることなく友達とのペアを作り終えることができるような交友関係について考察しました。
その結果、「全員友達」や「交友関係が正則な完全二部グラフ」といった、非現実的な(?)交友関係でないと、任意2人組作り可能とは言えないことがわかりました。

ここで、神経衰弱というトランプゲームについて考えてみましょう。通常の神経衰弱では、めくった2枚のカードの数字が同じであれば、その2枚を獲得することができます。この、カードを獲得できるかできないかについてのルールを変えることを考えます。
たとえば、「どんな2枚をめくったとしてもそれらを獲得することができる」というルールにしてみましょう。この場合、先手がすべてのカードをめくることで、カードが場に残ることなくゲームが終了します。あるいは、「めくった2枚のカードの数字と色が同じであれば、それらを獲得することができる」というルールを考えてみましょう。実はこの場合でも、どのような順番でカードをめくっていったとしても、すべてのカードをペアにすることができます。
では、どのようなルールであれば、ペアにできなかったカードが場に残ることがないといえるでしょうか。また、この際カードの枚数は52枚に限らず、適当な偶数枚であるとして考えましょう。
この問題は、2人組作りの問題と全く同じ問題になっています。このことは、これらの問題を次のように言い換えると明らかでしょう。

2人組作りの問題　偶数人のクラスで、どのような順番で2人組を作っても、全員があぶれることなく友達とのペアを作り終えることができるような交友関係は何か

神経衰弱の問題　偶数枚のカードで、どのような順番で2枚組を獲得しても、全てのカードを残すことなく獲得することができるようなルールは何か

実際、通常の神経衰弱においてペアにして取れるカードが隣接しているようなグラフを考えると、4点の完全グラフ13個の和になっているので、確かに任意2人組作り可能なグラフになっています(図1を参照)。このグラフはクラス内の交友関係として見るとかなり不自然(仲良し4人組が13組あり、それ以外に交友関係がない!)ですが、トランプ同士の関係として見ると自然ですね。

f:id:mel9:20191213001730p:plain:w450 — 図1

また、64枚の集合トランプにおける補集合神経衰弱を表すグラフは、4点の正則な完全二部グラフ16個の和になっています。

f:id:mel9:20191213004412p:plain:w450 — 図2

以上の考察から、任意2人組作り可能のことを神経衰弱可能とも呼ぶことにします。

1.2.ババ抜き可能とジジ抜き可能

ババ抜きについても同様に考えると、どのような順番でカードを捨てていっても最後に必ずJOKER一枚だけが残るようなルールは、神経衰弱可能なルールと一致します。したがって、神経衰弱可能のことをババ抜き可能とも呼ぶことにします。

すると、次のような疑問がわくのは自然です。

ジジ抜きの問題1　偶数枚のカードで、最初にどの1枚を捨て、その後どのような順番で2枚組を捨てても、最終的に1枚のカードだけが残るようにできるようなルールは何か
ジジ抜きの問題2　奇数枚のカードで、どのような順番で2枚組を捨てても、最終的に1枚のカードだけが残るようにできるようなルールは何か

ジジ抜きの問題1ではプレイする前の準備(ジジとなるカードを1枚抜く)も含めて考えており、問題2では準備は終わったものとして考えています。
ジジ抜きの問題1の条件を満たすルールを準備付きジジ抜き可能、ジジ抜きの問題2の条件を満たすルールを準備済みジジ抜き可能と呼ぶことにします。たとえば通常のジジ抜きを考えれば、4点の完全グラフ13個の和によって表されるルールは、準備付きジジ抜き可能です。3点の完全グラフ1個と4点の完全グラフ12個の和によって表されるルールは、準備済みジジ抜き可能です。

1.3.この記事の目標

トランプ52枚にJOKER1枚を加えた53枚に、次のようなルールを入れます。

JOKER以外の52枚のカードは、数字が同じであれば捨てられる(通常のババ抜きと同じ)
JOKERは任意のカードとのペアで捨てられる

このルールはWikipediaにて変形ジジ抜きとして紹介されています。すなわち、準備済みジジ抜き可能です。

また、次のグラフによって表されるグラフも準備済みジジ抜き可能です。

f:id:mel9:20191213012912p:plain:w450 — 図3

このグラフのように、いくつかの偶数点完全グラフ+1点の形になっているグラフはすべて準備済みジジ抜き可能です。ババ抜き可能のときよりも守備範囲が広くなっていることが見受けられます。特に準備済みジジ抜き可能に該当するグラフはかなり多くなることが予想されるので、まずは準備付きジジ抜き可能について考えることにしましょう。そして、この記事の最終目標は、準備付きジジ抜き可能なグラフをすべて決定することにします。今後、単にジジ抜き可能といった場合は準備付きジジ抜き可能を指すこととします。

1.4.グラフの言葉への書き換え

問題をグラフの言葉に書き換えておきます。

準備付きジジ抜きの問題　 $G$ を偶数個の点を持つグラフとする。グラフに対する操作1,2を次のように定める。

操作1　点を1つ選び、それを除去する。
操作2　辺を1つ選び、その両端点を除去する。

$G$ に対して操作1を1度行い、その後操作2を繰り返すことを考える。どのように点や辺を選んでも、点の個数が1個になるまで操作2を行い続けることができるようなグラフ $G$ の条件を求めよ。

それでは、次の章から実際に考察を進めていきましょう。

2.非連結の場合

2.1.ババ抜き可能なグラフはジジ抜き可能

この節では次の定理を証明します。

定理1
ババ抜き可能なグラフはジジ抜き可能である。

前記事の結果より、ババ抜き可能なグラフは次のものに限られます。

偶数点の完全グラフ
偶数点の正則な完全二部グラフ
2つのババ抜き可能なグラフの和

したがって、これらのグラフがジジ抜き可能であることを示せばよいことになります。ここでは、連結成分の個数に関する帰納法で証明します。

2.1.1.連結成分が1個の場合

偶数点の完全グラフ
偶数点の完全グラフ $K_{2n}$ から1点を除去すると、奇数点の完全グラフ $K_{2n-1}$ になります。これはどの2枚でもペアとして捨てられることを表現するグラフなので、当然準備済みジジ抜き可能です。

偶数点の正則な完全二部グラフ
偶数点の正則な完全二部グラフ $K_{n,n}$ から1点を除去すると、奇数点の完全二部グラフ $K_{n,n-1}$ になります。奇数点の完全二部グラフ $K_{n,n-1}$ が準備済みジジ抜き可能であることを帰納的に示しましょう。まず、 $K_{2,1}$ は明らかに準備済みジジ抜き可能です。次に、 $K_{n,n-1}$ から1辺と両端を除去することを考えます。このとき、図4のように、2つの独立集合(互いに隣接していない頂点の集合)から1点ずつ除去されることになります。元のグラフは完全二部グラフですから、除去後も完全二部グラフ、すなわち $K_{n-1,n-2}$ になります。したがって、 $K_{n-1,n-2}$ が準備済みジジ抜き可能ならば、 $K_{n,n-1}$ も準備済みジジ抜き可能です。

f:id:mel9:20191214172416p:plain:w450 — 図4

2.1.2.連結成分がn個の場合

連結成分がn-1個以下のババ抜き可能グラフはジジ抜き可能であると仮定します。
グラフ $G$ を連結成分がn個のババ抜き可能なグラフとすると、 $G$ は2つのババ抜き可能なグラフ $G_1$ と $G_2$ の和として表せます。 $G$ から1点を除去することを考えるとき、除去する点は $G_1$ の点だとして一般性を失いません。すると、帰納法の仮定より $G_1$ はジジ抜き可能ですから、 $G_1$ からどのような順番で辺と両端を除去しても、最終的に1点が残る状態まで除去をし続けることができます。また、 $G_2$ はババ抜き可能ですから、 $G_2$ からどのような順番で辺と両端を除去しても、最終的にすべての点を除去するまで除去をし続けることができます。したがって、グラフ $G$ はジジ抜き可能です。

以上より、ババ抜き可能なグラフはジジ抜き可能であることが証明できました。
つまり、トランプでババ抜きというゲームが成立した時点で、ジジ抜きという拡張ルールが破たんなく成立するのは決まっていた(?)のがわかります。もし異世界転生して、転生先でババ抜きのようなゲームを紹介されたら、ジジ抜きのような拡張ルールを提案してみましょう。そのルールは必ず問題なく成立するはずです。

2.2.奇数点完全グラフ2個の和はジジ抜き可能

奇数点完全グラフ2個の和は、ババ抜き可能ではありませんが、ジジ抜き可能になります。
奇数点完全グラフから1点を除くと偶数点完全グラフになるので、奇数点完全グラフ2個の和から1点を除くと、偶数点完全グラフと奇数点完全グラフの和になります。これは上の2.1.2.節での考察と同様にして、準備済みジジ抜き可能です。

2.3.それ以外の非連結グラフはジジ抜き不可能

上の二節の例で、ジジ抜き可能な非連結グラフは尽くされていることを証明しましょう。
$G$ を非連結なグラフで以下の条件を満たすものとします。
条件1　偶数点の完全グラフでも偶数点の正則な完全二部グラフでもない連結成分をもつ。
条件2　奇数点完全グラフ2個の和ではない。
このグラフ $G$ がジジ抜き不可能であることを証明します。グラフ全体は偶数点ですから、奇数点の成分はちょうど偶数個あることに注意して、以下のように場合分けをします。

2.3.1.連結成分が3個以上で、奇数点の成分が2個以上含まれるとき

このようなグラフには偶数点の成分が含まれるか、奇数点の成分が4個以上含まれます。前者なら偶数点の成分から、後者なら適当な成分から最初の1点を除去することにより、奇数点の成分が3つ以上残ります。すると、以降の操作は同一の成分から2点ずつ除去する操作になりますので、奇数点の成分からは必ず1点以上の孤立点が残ることになります。したがって、最終的に3点以上の孤立点が残ることになるので、このグラフはジジ抜き不可能になります。

2.3.2.奇数点の成分が含まれないとき

条件1より、ババ抜き不可能な成分が存在します。そのような成分を一つ選んで $G_1$ とします。 $G_1$ 以外の成分からはじめの1点を除去すると、その成分は奇数点になるので、その成分から1点以上の孤立点が残ることになります。 $G_1$ はババ抜き不可能ですから、2点以上の孤立点が残るような除去の仕方が存在します。したがって、このグラフはジジ抜き不可能です。

2.3.3.連結成分が2個で、両方とも奇数点のとき

条件2より、少なくとも一方の成分は完全グラフではありません。この完全グラフでない成分からはじめの1点を除去することを考えましょう。ここで、次の補題を証明します。

補題2

グラフ $G$ は連結グラフであるとする。このグラフから1点を除去するとき、除去する点を適切に選べば、除去した後のグラフが連結になるようにできる。
グラフ $G$ は奇数点の連結グラフで、完全グラフではないとする。このグラフから1点を除去するとき、除去する点を適切に選べば、除去した後のグラフがババ抜き不可能なグラフになるようにできる。

1の証明です。 $G$ の全域木のうち1つを適当に選んで固定します。この全域木において次数1の点を適当に1つ選んで除去すると、残りのグラフは連結です。
2の証明です。1により、除去した後のグラフが連結になるように1点を選べます。これを除去したグラフがババ抜き不可能ならば、この点を除去すれば良いので終了です。もしこれを除去したグラフがババ抜き可能ならば、元のグラフは連結なババ抜き可能グラフに1点を付け加えた形になっています(図5参照)。

f:id:mel9:20191214233649p:plain:w300 — 図5

したがって、元のグラフの点数を $2n+1$ とすると、その次数列は

$\{k,2n,\ldots ,2n,2n+1,\ldots ,2n+1\} \ (k\leq 2n-1, 次数2n+1の点はk個)$
$\{k,n,\ldots ,n,n+1,\ldots ,n+1\} \ (k\leq n, 次数n+1の点はk個)$
$\{n,\ldots ,n,n+1,\ldots ,n+1,k\} \ (k\geq n+1, 次数n+1の点はk個)$

のいずれかとなります。一番上の場合は次数2nの点を除去すれば、次数kの点と次数2nの点が残るので、除去後のグラフはババ抜き不可能です。真ん中の場合は次数n+1の点を除去すれば、次数n以上の点と次数k-1の点が残るのでOKです。次数nの点と一番下の場合は次数nの点を除去すれば、次数n以下の点と次数kの点が残るのでこれもOKです。これで、補題2は証明終了です。
元の証明に戻ります。完全グラフでない成分から補題2-2の条件を満たすような点を除去すると、その成分からは2点以上、もう一方の成分からは1点以上の孤立点が残るような除去の方法が存在するので、元のグラフはジジ抜き不可能です。

以上により、ジジ抜き可能な非連結グラフが決定できました。

定理3
以下のグラフはジジ抜き可能であり、ジジ抜き可能な非連結グラフは以下のものに限られる。

ババ抜き可能なグラフ。すなわち偶数点完全グラフと正則な完全二部グラフ、またはその和
奇数点完全グラフ2個の和

3.連結グラフに関する考察の方針

3.1.独立集合の大きさが高々2であるグラフはジジ抜き可能

この節では次の定理を説明します。

定理4
偶数点のグラフ $G$ が大きさが3の独立集合を持たないならば、 $G$ はジジ抜き可能である。

ここで独立集合とは、互いに隣接しない点集合のことです(たとえば下図6の{A,B,C}は独立集合)。また、「大きさが3の独立集合を持たない」という条件は、「補グラフが三角形を含まない」とも言い換えられます。

f:id:mel9:20191218125951p:plain:w200 — 図6

あるグラフ $G$ がジジ抜き不可能であることは、ある順番で操作を行ったとき、最終的に3以上の奇数個の点が孤立点として残ることを意味します。ここで、最終的に孤立点として残る点の集合は、もともとのグラフでは独立集合であるはずです。したがって、はじめから3点の独立集合が存在しなければ、そのグラフはジジ抜き可能であるはずです。したがって、たとえば完全グラフから1辺を除いたグラフはジジ抜き可能です。

f:id:mel9:20191218142943p:plain:w200 — 図7 大きさが3の独立集合を持たないグラフの例。完全グラフから八角形を除いた形になっているので、補グラフは八角形。すなわち、三角形を含まない。

3.2.完全マッチングを使った問題の言い換え

今回も前記事と同様に、点の個数に関する帰納法を用いて考察を行いたいのですが、ジジ抜きの場合ははじめに1点除去するという操作が入るので、そのままでは帰納法を用いることができません。この問題を克服するため、問題の言い換えを行います。

定理5
偶数点のグラフ $G$ について、以下の2条件は同値である。
条件1 $G$ はジジ抜き可能である。
条件2 任意の3以上の奇数点の独立集合とそれに含まれない1点に対して、これらの点をすべて除去した後のグラフには完全マッチングが存在しない。

ここで、2n点のグラフの完全マッチングとは、互いに端点を共有しない辺の集合で、大きさがnであるもののことです。たとえば、下図8で赤色になっている辺の集合は完全マッチングです。また、0点のグラフには完全マッチングが存在するものとします。

f:id:mel9:20191218144301p:plain:w200 — 図8

条件2について説明します。前節では、3点の独立集合が初めから存在しなければジジ抜き可能であることを説明しました。もし、3点の独立集合があったとしても、それが残るような操作が行えなければジジ抜き可能です。この条件2は、どんな奇数点の独立集合についても、それが残るような操作が行えないということを言っています。下の図9でいえば、 $\{A,C,E\}$ と $\{B,D,F\}$ はそれぞれ3点の独立集合です。しかし、どのような順番で操作を行っても、 $\{A,C,E\}$ や $\{B,D,F\}$ が最後に残るようにはできません。

f:id:mel9:20191218145233p:plain:w200 — 図9 これは6点の正則完全二部グラフ

逆に、ある3以上の奇数点の独立集合 $X$ とそれに含まれない1点 $A$ に対して、これらの点をすべて除去した後のグラフに完全マッチングが存在することを仮定します(すなわち、条件2の否定)。すると、はじめに点 $A$ を除去し、完全マッチングに従って辺と両端を除去していくことで、最後に3以上の奇数個の孤立点 $X$ が残るようにできます。したがって、元のグラフはジジ抜き不可能です。下の図10では、3点の独立集合 $\{B,D,F\}$ と点 $A$ を除去したグラフには、完全マッチング $\{CE\}$ が存在します。初めに点 $A$ を除去し、次に辺 $\{CE\}$ を除去することで、最後に孤立点 $\{B,D,F\}$ が残ります。

f:id:mel9:20191218150235p:plain:w200 — 図10

3.3.ジジ抜き不可能の再帰的な言い換え

前節で示した言い換えにおいて、各条件の否定を取ると、次のようになります。

定理5'
偶数点のグラフ $G$ について、以下の2条件は同値である。
条件1 $G$ はジジ抜き不可能である。
条件2 ある3以上の奇数点の独立集合とそれに含まれない1点が存在して、これらの点をすべて除去した後のグラフには完全マッチングが存在する。

これを用いて、次の定理を証明します。これによって、グラフがジジ抜き不可能であることを帰納的に示せるようになります。

定理6
空でない6以上の偶数点のグラフ $G$ について、以下の2条件は同値である。
条件1 $G$ はジジ抜き不可能である。
条件2 ある1辺が存在して、その辺と両端を除去した後のグラフがジジ抜き不可能である。

条件1から条件2
3以上の奇数点の独立集合 $X$ とそれに含まれない1点 $A$ に対して、これらの点をすべて除去した後のグラフには完全マッチング $M$ が存在するとします。除去した後のグラフが0点のグラフならば、元のグラフは星と孤立点の集合です。星とは、完全二部グラフ $K_{1,n}$ のことです。星から1辺と両端を除去すると空グラフになるので、除去後のグラフはジジ抜き不可能となります。除去後のグラフに点が存在するならば、その完全マッチング $M$ は空集合ではありません。その中から1辺 $v$ を選びます。この辺と両端を除去したグラフは、3以上の奇数点の独立集合 $X$ とそれに含まれない1点 $A$ に対して、これらの点をすべて除去した後のグラフには完全マッチング $M-\{v\}$ が存在するので、ジジ抜き不可能です。

条件2から条件1
1辺 $v$ と両端を除去した後のグラフがジジ抜き不可能とします。この除去後のグラフにおいて、3以上の奇数点の独立集合 $X$ とそれに含まれない1点 $A$ に対して、これらの点をすべて除去した後のグラフには完全マッチング $M$ が存在するとします。すると、最初のグラフは3以上の奇数点の独立集合 $X$ とそれに含まれない1点 $A$ に対して、これらの点をすべて除去した後のグラフには完全マッチング $M+\{v\}$ が存在するので、ジジ抜き不可能です。

続く4章では、この定理6を用いて、ジジ抜き可能なグラフを決定します。

4.連結の場合

4.1.グラフが6点の場合

帰納法のもととするために、6点のグラフについて全探索を行って、ジジ抜き可能なものを探します。定理6より、全探索は4点で行えば十分である気もしますが、後々面倒になるので6点で全探索をしてしまいます。なお、6点の連結単純グラフは112種類あります。
全探索の結果、3点の独立集合を持つにもかかわらずジジ抜き可能な6点の連結グラフは、以下の4つのみとなりました。

f:id:mel9:20191218153922p:plain:w400 — 図11

これらのグラフの特徴を探ってみましょう。左上のグラフは6点の正則な完全二部グラフです。他のグラフも、左上のグラフからいくつかの辺を除去した形になっているので、点集合を3点+3点の独立集合に分割できる二部グラフです。
ここで、右下のグラフを図12のように書き換えてみましょう。図12において、上の3点と下の3点はそれぞれ独立集合です。そして、図12のグラフはこの2つ以外に3点の独立集合をもちません。図11の他のグラフも、これと同様の特徴をもちます。次の節では、このような特徴をもつグラフがジジ抜き可能であることを示します。

f:id:mel9:20191228085841p:plain:w200 — 図12

4.2. 2つの独立集合以外に3点以上の独立集合をもたない二部グラフはジジ抜き可能

節の表題ではあいまいな(正しくない)表現をしていますが、要は次の定理7が成り立ちます。

定理7
グラフ $G$ は二部グラフであって、その点集合 $V$ を2つの独立集合 $X$ と $Y$ に分割したとき、 $X$ の大きさと $Y$ の大きさが等しいとする。このとき、 $G$ が次の条件を満たすならば、 $G$ はジジ抜き可能である。
条件 $V$ の任意の部分集合 $U$ に対して、 $U$ が3点以上の独立集合ならば、 $U\subset X$ または $U\subset Y$ である。

証明
$G$ の点の数に関する数学的帰納法により示す。
2点および4点のグラフに対しては、そもそも定理の条件を満たすグラフが3点以上の独立集合をもたないものに限られるため、定理7の主張が成り立つ。
2n点以下のグラフに対して、定理7の主張が成り立つと仮定する。 $G$ を2n+2点のグラフとし、定理の条件を満たすとする。ここで定理6の条件1および2の否定をとると、次のようになる。

定理6'
空でない6以上の偶数点のグラフ $G$ について、以下の2条件は同値である。
条件1 $G$ はジジ抜き可能である。
条件2 任意の辺に対して、その辺と両端を除去した後のグラフがジジ抜き可能である。

ここで、 $G$ が条件2を満たすことを示す(参考:図13)。
$G$ から適当な一辺 $vw$ と両端を除去したグラフを考える。元のグラフは二部グラフなので、 $v\in X, w\in Y$ としてよい。除去後のグラフ $G'$ は再び二部グラフで、大きさの等しい2つの独立集合 $X-\{v\}$ と $Y-\{w\}$ に分割できる。
$U$ が $V-\{v,w\}$ の部分集合であって、3点以上の独立集合であるとする。すると $U$ は $V$ の部分集合でもあるので、定理の条件より $U\subset X$ または $U\subset Y$ である。 $U$ は $v$ や $w$ を含まないから、 $U\subset X-\{v\}$ または $U\subset Y-\{w\}$ である。
したがって、除去後のグラフは定理の条件を満たすので、帰納法の仮定よりジジ抜き可能である。
したがって、 $G$ は定理6'の条件2を満たすので、ジジ抜き可能である。(証明おわり)

f:id:mel9:20191228100058p:plain:w250 — 図13

連結グラフでジジ抜き可能だと判明したものについてまとめます。

まとめ
以下のグラフはジジ抜き可能である。

3点の独立集合を持たないグラフ
二部グラフ $G=(V=X+Y, E)$ で、 $|X|=|Y|$ であり、 $X$ と $Y$ 以外に3点の独立集合を持たないグラフ

ここに、連結なババ抜き可能グラフとの対応関係を見て取れます。

ババ抜き可能	ジジ抜き可能
完全グラフ	3点以上の独立集合を持たないグラフ
正則な完全二部グラフ	$X$ と $Y$ 以外に3点の独立集合を持たない二部グラフ

連結なババ抜き可能グラフはこの表に挙げられているものに限られましたが、実は連結なジジ抜き可能グラフもこれらに限られます。これを次の節から示していきます。

4.3. 2つの独立集合以外に3点以上の独立集合をもたない二部グラフであることと同値な条件

この節では、定理7の条件を満たすことが、すべての点の次数がn-1以上であることと同値であることを証明します。

補題8
グラフ $G$ は2n点の二部グラフであって、その点集合 $V$ を2つの独立集合 $X$ と $Y$ に分割したとき、 $X$ の大きさと $Y$ の大きさが等しいとする。このとき、次の2条件は同値である。
条件1 $V$ の任意の部分集合 $U$ に対して、 $U$ が3点以上の独立集合ならば、 $U\subset X$ または $U\subset Y$ である。
条件2 $G$ のすべての点の次数はn-1以上である。

n=1のときはすべてのグラフが条件1と2をともに満たす。以下では $n\geq 2$ とする。
条件1から条件2
対偶を示す。 $G$ の点 $v$ の次数がn-2以下であるとする。 $v\in X$ としてよい。 $Y$ には $v$ と隣接しない点が少なくとも2つある。 $Y$ の点 $w_1$ と $w_2$ が $v$ と隣接していないとする。このとき、 $\{v, w_1, w_2\}$ は3点の独立集合であるが、 $X$ にも $Y$ にも含まれない。

条件2から条件1
対偶を示す。 $U$ が3点以上の独立集合であって、 $X$ と $Y$ の両方と共通部分をもつとする。 $U$ と $Y$ が2点 $w_1, w_2$ を共有するとしてよい。 $v\in U\cap X$ とすると、 $v$ の次数はn-2以下である。(証明終わり)

要するに条件1や2を満たすグラフにおいては、 $X$ の点 $v$ と隣接しない $Y$ の点は高々1個ってことですね(この考え方を補題12の証明で用います)。
ここで、今後の表記を簡略化するために、 $B_{m,n}$ 、 $_kB_{m,n}$ という記号を以下のように導入します。この定義はこの記事独自のものであり、他では全く通用しません。もしこれと同じ(似た)概念を表す一般的な用語をご存知の方がいらっしゃれば、コメント欄などでご教示いただけるとありがたいです。

定義9
グラフ $G$ が次の条件をみたすとき、 $G$ は $B_{m,n}$ であるという。

$m+n$ 点をもつ。
互いに素な点集合 $X,Y$ であって、その大きさがそれぞれ $m,n$ であるようなものが存在する。

これに加えて次の条件もみたすとき、 $G$ は $_kB_{m,n}$ であるという。

すべての点の次数はk以上である。

定義7の2番目の条件から、 $B_{m,n}$ なグラフは二部グラフです。また、この記号は完全グラフを表す $K_n$ などとは違い、特定の1つのグラフを表すわけではないことに注意してください。

補題8の結果とこの記法を用いると、前節のまとめは以下のようになります。

まとめ
以下のグラフはジジ抜き可能である。

3点の独立集合を持たないグラフ
$_{n-1}B_{n,n}$ グラフ

4.4. 帰納法を回す

この節では次の補題10を示し、定理6を用いて、ジジ抜き可能な連結グラフは前節でまとめたものに限られることを示します。途中、場合分けの深さが5くらいになるところがありますが、がんばりましょう。

補題10
$n\geq 4$ とする。グラフ $G$ は2n点の連結グラフであって、3点の独立集合をもち、 $_{n-1}B_{n,n}$ ではないとする。このとき、ある1辺が存在して、その辺と両端を除去したグラフが次の条件のいずれかをみたすようにできる。
条件1 連結グラフであって、3点の独立集合をもち、 $_{n-2}B_{n-1,n-1}$ でもない
条件2 非連結グラフであって、ジジ抜き不可能

まずはこれをかなり緩めた補題11を示します。

補題11
グラフ $G$ は8点以上の連結グラフであって、3点の独立集合をもち、 $_{n-1}B_{n,n}$ ではないとする。このとき、ある1辺が存在して、その辺と両端を除去したグラフが3点の独立集合を持つようにできる。

証明
$U\subset V$ を3点の独立集合とする。 $U$ に含まれない2点を結ぶ辺が存在すれば、その辺と両端を除去したグラフは3点の独立集合 $U$ をもつ。 $U$ に含まれない2点を結ぶ辺が存在しないとき、 $V-U$ は5点以上の独立集合である。したがって、どの辺と両端を除去しても、除去後のグラフは4点以上の独立集合をもつ。(補題11証明終わり)

除去後のグラフが3点の独立集合を持つような辺を適当に1つ選び、その辺と両端を除去します。このとき、除去後のグラフはつぎのうちのいずれかであるでしょう。

3点の独立集合をもち、連結で $_{n-2}B_{n-1,n-1}$ なグラフ
3点の独立集合をもち、連結で $_{n-2}B_{n-1,n-1}$ ではないグラフ
3点の独立集合をもち、非連結でジジ抜き可能なグラフ
3点の独立集合をもち、非連結でジジ抜き不可能なグラフ

2番や4番になった場合は、ここで除去した辺が補題10の条件にかなう辺ですので、これ以上考察不要です。1番や3番になった場合に、また別の辺を選んで、除去後のグラフが補題10の条件1または2を満たすようにできることを示します。

1. 除去後のグラフが3点の独立集合をもち、連結で $_{n-2}B_{n-1,n-1}$ なグラフになった場合
まずは次の補題を示します。

補題12
グラフ $G$ は6点以上の点をもち、 $_{n-1}B_{n,n}$ であるとする。 $G$ は長さ2nの閉路を持つ。

証明
$G$ の大きさnの独立集合を $X,Y$ とする。 $X,Y$ の中で、次数n-1の点の集合を $X_1,Y_1$ 、次数nの点の集合を $X_2,Y_2$ とする。このとき、 $G$ の各点に次のように名前を付けることができる。

$X_1$ に属する点には、適当に $a_1, a_2, \ldots , a_k$ と名付ける。 $X_2$ に属する点には、適当に $a_{k+1}, a_{k+2}, \ldots , a_n$ と名付ける。
$Y_1$ に属する点のうち、 $a_i$ と隣接しない点には $b_i$ と名付ける。 $Y_2$ に属する点には、適当に $b_{k+1}, b_{k+2}, \ldots , b_n$ と名付ける。

ここで $n\geq 3$ より、 $a_1 b_n a_2 b_1 a_3 \ldots b_{n-2} a_n b_{n-1} a_1$ は長さ2nの閉路である。(補題12証明おわり)

補題10の証明に戻ります。
1.1. 元のグラフが二部グラフでないとき
除去後のグラフの大きさがn-1の独立集合を $X, Y$ とする。また、除去された2点を $v,w$ とする。このとき元のグラフは、次の2条件のどちらかを満たすとしてよい。

$v$ は $X, Y$ の両方と隣接していて、 $w$ はどちらとも隣接していない。
$v$ と $w$ がともに $X$ に隣接している。

この2つで場合分けをする。

1.1.1. $v$ は $X, Y$ の両方と隣接していて、 $w$ はどちらとも隣接していないとき
前者の場合、除去後のグラフで $w$ が孤立するように辺を選ぶことができる(図14を参照)。そのとき、 $w$ が含まれないほうの成分は明らかに完全グラフではないから、この除去によってできるグラフは非連結なジジ抜き不可能グラフである。

f:id:mel9:20191228121048p:plain:w250 — 図14 赤い辺と両端を除去するとwが孤立する

1.1.2. $v$ と $w$ がともに $X$ に隣接しているとき
元のグラフが10点以上の場合と8点の場合に分けて示す。

1.1.2.1. 元のグラフが10点以上の場合
$v, w$ を除去することで $_{n-2}B_{n-1,n-1} (n\geq 5)$ なグラフになったことから、元のグラフは2つの互いに素な4点の独立集合をもつ。したがって、どの辺と両端を除去しても除去後のグラフは3点の独立集合をもつ。
補題12より、 $v, w$ を除去したグラフには長さ2nの閉路が含まれる(図15参照)。この長さ2nの閉路を一つ選んで固定する。元のグラフに対する仮定より、閉路上での距離が偶数の点 $x, y$ で、 $v$ と $x$ 、 $w$ と $y$ がそれぞれ隣接しているようなものが存在する。ただし、 $x=y$ である場合に注意。ここで、閉路上の $x$ から $y$ への道のうち、長い方の長さは4以上である(長さ0のものも道と呼んでいる)。この長い方の道に属する辺のうち、端点に $x, y$ を含まない辺と両端を除去することで、除去後のグラフは長さが奇数の閉路 $y\rightarrow w\rightarrow v\rightarrow x\rightarrow 短い方の道 \rightarrow y$ を含むようになる。したがって、除去後のグラフは二部グラフではないので、 $_{n-2}B_{n-1,n-1}$ でもない。さらに、この除去後のグラフは連結である。

f:id:mel9:20191228122155p:plain:w200 — 図15 赤い辺を除去すると、除去後のグラフは二部グラフではなくなる

1.1.2.2. 元のグラフが8点の場合
補題12より、 $v, w$ を除去したグラフには長さ2nの閉路が含まれる。この長さ2nの閉路を一つ選んで固定し、各頂点に1~6の番号を順番に振る(図16,17参照)。このとき、元のグラフは次の2条件のどちらかを満たすとしてよい。

$v$ が1と隣接し、 $w$ が3と隣接する(図16)。
$v, w$ がともに1と隣接する(図17)。

前者(図16)のとき、ある辺と両端を除去することで、残りのグラフが補題10の条件1をみたすことを示す。
第一に、点2,4,6のうち $v$ と隣接している点が高々1個のときを考える。 $v$ と4が隣接するときは辺45を除去すれば、残りのグラフは連結で、2,6,vが独立集合となり、閉路123wvをもつので二部グラフではなくなる。 $v$ と6が隣接するときも同様。 $v$ が4とも6とも隣接しないときは辺12を除去すれば、残りのグラフは連結で、4,6,vが独立集合となり、vの次数は1であるから、 $_{2}B_{3,3}$ ではなくなる。点2,4,6のうち $w$ と隣接している点が高々1個のときも同様である。
第二に、点2,4,6のうち $v$ と隣接している点が2個以上あり、かつ、点2,4,6のうち $w$ と隣接している点が2個以上ある場合を考える。 $v$ が6と隣接しているとしてよい。このとき、辺6vを除去すれば、残りのグラフは連結で、1,3,5が独立集合となる。 $w$ は2と4のうち少なくとも一方と隣接しているから、残りのグラフは奇数点の閉路をもつ。すなわち、二部グラフではない。

f:id:mel9:20191228124949p:plain:w200 — 図16

後者(図17)のときも、図16のときの証明とほぼ同じだから省略する( $v$ が4とも6とも隣接しないときに除去する辺を辺23にすれば良いだけである)。

f:id:mel9:20191228125249p:plain:w200 — 図17

1.2. 元のグラフが二部グラフであるとき
除去後のグラフの大きさがn-1の独立集合を $X, Y$ とする。また、除去された2点を $v,w$ とする。さらに、 $v$ と $X$ の点は隣接せず、 $w$ と $Y$ の点は隣接しないとする。ここで、 $w$ が $X, Y$ のどちらとも隣接していないときは、1.1.1の場合と同様に、 $w$ が孤立点になり、 $w$ が含まれない方の成分が完全グラフにならないような除去の仕方が存在する(図18)。

f:id:mel9:20191229012843p:plain:w150 — 図18

$w$ が $X$ の点と隣接していて、 $v$ が $Y$ の点と隣接している場合を考える(図19,20)。元のグラフは $_{n-1}B_{n,n}$ ではないので、次数がn-2以下の点が存在する。そのような点を1つ選び、 $x$ とする。ここで、 $x\in X+\{v\}$ としてよい。 $Y+\{w\}$ には $x$ と隣接しない点が2個以上存在する。このような点を2個選んで $y_1, y_2$ とする。 $Y-\{y_1, y_2\}$ に属する点を1つ選び $y$ とする(元のグラフは8点以上をもつから、 $Y-\{y_1, y_2\}$ は空でない)。ここで、2点 $v,w$ を除去したグラフは $_{n-2}B_{n-1,n-1}$ だから、元のグラフにおいて $X$ や $Y$ に属する点の次数はn-2以上である。したがって、 $X+\{v\}-\{x\}$ の元であって、 $y$ と隣接するものが存在する。そのような点を1つ選び、 $z$ とする。ただし、 $v$ と $y$ が隣接しているときは $z=v$ とする(図20)。ここで、2点 $y, z$ を除去すると、残りのグラフが補題10の条件1を満たすことを示す。まず、元のグラフは8点以上の二部グラフであるから、2つの互いに素な4点の独立集合をもつ。したがって、どの2点を除去したとしても、残りのグラフは3点の独立集合をもつ。
$z\neq v$ の場合(図19)。元のグラフから $v, w, y, z$ の4点を除去したグラフは、定理7の証明より、 $_{n-3}B_{n-2,n-2}$ である。したがって補題12より、 $v, w, y, z$ の4点を除去したグラフには長さ2n-4の閉路が存在するので連結。元のグラフにおいて $v$ と $Y$ の点は隣接し、 $v$ と $y$ は隣接していないから、 $v$ と $Y-\{y\}$ の点は隣接している。また、 $w$ と $v$ は隣接している。したがって、元のグラフから $y, z$ の2点を除去したグラフは連結である。また、 $x$ は $y_1, y_2$ と隣接しないから次数n-3以下である。すなわち、残りのグラフは $_{n-2}B_{n-1,n-1}$ ではない。

f:id:mel9:20191229015510p:plain:w350 — 図19

$z=v$ の場合(図20)。図19の場合と同様に考えれば残りのグラフは連結であり、 $_{n-2}B_{n-1,n-1}$ ではない。

f:id:mel9:20191229015543p:plain:w350 — 図20

ここまでで、1番の「3点の独立集合をもち、連結で $_{n-2}B_{n-1,n-1}$ なグラフになった場合」について、残りのグラフが補題10の条件1または2を満たすような除去が存在することが示せました。つづいて3番の「除去した残りのグラフが3点の独立集合をもち、非連結でジジ抜き可能なグラフになった場合」について考えましょう。このとき、残りのグラフが(補題10の条件1を満たさなくても、)3点の独立集合をもつ連結グラフになるような除去が存在することが示せれば、1番や2番の状況に帰着できます。したがってここでは、残りのグラフが、3点の独立集合をもつ連結グラフまたは、非連結なジジ抜き不可能グラフになるような除去が存在することを証明します。

3. 除去後のグラフが3点の独立集合をもち、非連結でジジ抜き可能なグラフになった場合
除去された2点を $v,w$ とする。奇数点の完全グラフ2個の和は3点の独立集合を持たないことに注意して、以下の4通りに場合分けをする。

除去後のグラフが $K_{2m} (m\geq 2)$ を含むとき
除去後のグラフが $K_{2m} (m\geq 2)$ を含まず、 $K_{m,m} (m\geq 3)$ を含むとき
除去後のグラフが $K_{2m} (m\geq 2)$ も $K_{m,m} (m\geq 3)$ も含まず、 $K_{2,2}$ を含むとき
除去後のグラフが $K_{2m} (m\geq 2)$ も $K_{m,m} (m\geq 2)$ も含まないとき

3.1. 除去後のグラフが $K_{2m} (m\geq 2)$ を含むとき
元のグラフにおける3点の独立集合を適当にとる。この3点のうち $K_{2m}$ に含まれるのは高々1点である。また、 $K_{2m}$ には $v, w$ の少なくとも一方と隣接している点が少なくとも1点存在する。これらの点を避けて、 $K_{2m}$ から除去する辺を選ぶと、除去後のグラフは連結で3点の独立集合をもつ。

f:id:mel9:20191229023225p:plain:w300 — 図21 {1,2,3}が独立集合で、4がv,wに隣接する点。1,4が端点に来るものを避けて、左のK_4から除去する辺を選べばよい。

3.2. 除去後のグラフが $K_{2m} (m\geq 2)$ を含まず、 $K_{m,m} (m\geq 3)$ を含むとき
$K_{m,m} (m\geq 3)$ をひとつ選んで固定する。それ以外の部分から、非連結にならないように辺を選んで除去すれば良い(図22の赤い辺を除去する)。

f:id:mel9:20191229025229p:plain:w220 — 図22

3.3. 除去後のグラフが $K_{2m} (m\geq 2)$ も $K_{m,m} (m\geq 3)$ も含まず、 $K_{2,2}$ を含むとき
まず、元のグラフが10点以上をもつときを考える。除去後のグラフが $K_2$ をもつならば、その2点を除去すれば、除去後のグラフは3点の独立集合をもつ連結グラフになる(図23)。

f:id:mel9:20200506194839p:plain:w160 — 図23 除去後のグラフがK2,2と2つのK2になる場合

除去後のグラフが $K_2$ をもたない(すなわち $K_{2,2}$ だらけ)ならば、次のように辺を選んで除去すれば、除去後のグラフは3点の独立集合をもつ連結グラフになる(図24)。

除去後のグラフの $K_{2,2}$ をひとつ選んで固定する。この $K_{2,2}$ に含まれる4つの点のうち、元のグラフにおいて $v$ に隣接していたものを1つ選び、 $x$ とする(必要なら $v$ と $w$ の記号を入れ替える)。この $K_{2,2}$ に含まれる4つの辺のうち、点 $x$ を端点にもたないような辺を1つ選び、これを除去する。

f:id:mel9:20200506194920p:plain:w160 — 図24 除去後のグラフが2つのK2,2になる場合

元のグラフが8点の場合を考える。この場合、除去後のグラフは $K_{2,2}$ と $K_2$ の和である。元のグラフにおいて点 $v, w$ と $K_{2,2}$ の間に伸びていた辺の本数がそれぞれ高々1本であったとする。 $K_2$ の2点を除去すれば、除去後のグラフは3点の独立集合をもつ連結グラフになる(図25)。

f:id:mel9:20200506195006p:plain:w160 — 図25

元のグラフにおいて、 $v, w$ の両方がこの $K_{2,2}$ との間に2本以上の辺を有していたとする。必要ならば $v$ と $w$ の名前を入れ替えることにより、元のグラフで $v$ が $K_2$ に隣接していたとしてよい。このとき、 $w$ と $K_{2,2}$ との間に伸びる辺の中から、除去しても非連結にならないものが選べる。これを選んで除去すれば、除去後のグラフは3点の独立集合をもつ連結グラフになる(図26)。

f:id:mel9:20200506195036p:plain:w160 — 図26

3.4. 除去後のグラフが $K_{2m} (m\geq 2)$ も $K_{m,m} (m\geq 2)$ も含まないとき
要するに除去後のグラフが $K_2$ だらけのときである。 $K_2$ が4個以上あるときはそのうち1個を除去すれば連結で3点の独立集合をもつグラフになる(図27)。

f:id:mel9:20191229035825p:plain:w200 — 図27 赤い辺と両端を除去する。たとえば赤い3点が独立集合になる。

$K_2$ が3個のときを考える。もはや除去後が $K_2$ ×3のグラフになる場合以外については代替の除去法を探し終えたので、除去後のグラフが「3点の独立集合をもち、 $K_2$ ×3ではない」グラフになるような除去が見つかりさえすればよい。3つの $K_2$ のうち、 $v$ との間に辺が伸びているものの個数を $f(v)$ と書く。 $f(w)$ も同様に定める。 $f(v)$ と $f(w)$ の両方が3であるときは、 $v$ を端点とする辺のうち $vw$ でないものを適当に1つ選んで除去すれば、除去後のグラフは3点の独立集合をもち、連結または孤立点をもつ。連結なグラフも、孤立点をもつグラフも、 $K_2$ ×3ではない(図28)。

f:id:mel9:20200506195149p:plain:w160 — 図28 f(v)=f(w)=3の場合。vを端点とする4つの辺(赤い辺)のどれを選んでも良いことがわかる。

$f(v)$ と $f(w)$ の少なくとも一方が3ではないときを考える。 $f(w)$ が3でないとしてよい。このとき、 $w$ との間に辺をもたない $K_2$ に属する点のうち、 $v$ と隣接するものを1つ選んで $x$ とする。ここで、 $xv$ を選んで除去すれば、除去後のグラフは3点の独立集合をもち、孤立点をもつ。さきほどと同様、孤立点をもつグラフは $K_2$ ×3ではない(図29)。

f:id:mel9:20200506195241p:plain:w160 — 図29 f(v)=2、f(w)=2の例

これで補題10が示せました！そして定理6を利用した数学的帰納法により、ジジ抜き可能な連結グラフが次のように決定できます！

定理13
以下のグラフはジジ抜き可能であり、ジジ抜き可能な連結グラフは以下のものに限られる。

3点の独立集合を持たないグラフ
$_{n-1}B_{n,n}$ グラフ

5.結論

ジジ抜き可能なグラフを改めてまとめると、以下のようになります。

まとめ
以下のグラフはジジ抜き可能であり、ジジ抜き可能な連結グラフは以下のものに限られる。

3点の独立集合を持たないグラフ
$_{n-1}B_{n,n}$ グラフ( $X$ と $Y$ 以外に3点の独立集合を持たない二部グラフ)

以下のグラフはジジ抜き可能であり、ジジ抜き可能な非連結グラフは以下のものに限られる。

奇数点の完全グラフ2個の和で表せるグラフ(3点の独立集合を持たないグラフ)
ババ抜き可能なグラフ

ジジ抜き可能であることには、そもそもグラフが3点の独立集合を持たないということが強く効いており、逆に3点の独立集合をもつようなグラフは多くがジジ抜き不可能であることがわかりました。

6.今後の展望

これに関連して考えてみたいことや思いついたことを列挙します。
まあまずはもう少し簡潔な証明を考えたいですね。4節の最後のほうはとりあえず示せればいいやという気持ちでやっていたので、グダグダと場合分けを増やしてしまいました。さすがにもっと楽な方法がありそうです。

6.1. ババ抜き可能やジジ抜き可能のさらなる別解釈

ババ抜き可能は神経衰弱可能や任意2人組作り可能に読み替えることができました。これらのほかにも、ババ抜きと似たような構造をもつゲームや状況があるかもしれません。とくにトランプゲームでペアを作っていくゲームは他にもありそうです(が、私はこの2つしか思い浮かびませんでした)。もし、なにか思いつく方がいらっしゃいましたら、コメント欄などで教えてください。

6.2. 欠席者と先生付きの2人組作りの問題

ジジ抜き可能は、次のようにすれば2人組作りの言葉に読み替えることができます。

欠席者1人と先生1人付き2人組作りの問題　偶数人の生徒がいるクラスで2人組を作る。しかし、今日は1人だけ欠席者がいて、どのように2人組を作っても少なくとも1人はあぶれてしまう。そこで、あぶれた人が1人だけならば、先生がその人と2人組を組むことができることにしよう。誰が欠席したかにかかわらず、どのような順番で2人組を作っても、最終的に誰もあぶれることがなく2人組を作り終えられるような交友関係は何か。

これを欠席者1人と先生1人付き2人組作りの問題と呼びましょう。この問題の答えはジジ抜きの問題と同じになります。では、欠席者m人と先生n人付き2人組作りの問題の答えはどうなるでしょうか。直感的には、欠席者と先生が増えるごとに条件がどんどんゆるくなる気がします。というのも、欠席者も先生もいない2人組作りの問題では完全グラフと正則完全二部グラフ以外ダメであるという結論だったのが、欠席者と先生が1人ずつ入ったことで少し条件がゆるくなったからです。また、2n人のクラスで欠席者n人と先生n人がいれば、どのような交友関係であっても(交友関係が空グラフであっても)2人組作り可能になります。もはやクラスで2人組作りをしていると言えるのかはわかりませんが......。

ところで、たとえば欠席者0人と先生2人付き2人組作りの問題をババ抜きの言葉に直すと次のようになります。

欠席者0人と先生2人付き2人組作りの問題(ババ抜き版)　偶数枚のカードにJOKERを加えてババ抜きをする。どのような順番で2枚組を捨てても、最終的に1枚ないし3枚のカードだけが残るようにできるようなルールは何か

これはルールとして少しおかしいですね。最悪の場合、3人が1枚ずつペアにならないカードをもった状態になり、その後の手番によって敗者が決まるという、つまらないゲームになってしまいます。
このように、ある表現では現実味を帯びた問題でも、別の表現に直すとおかしな問題になってしまう場合があるので、6.1.節で述べたような言い換えが重要になります。

6.3. 3人組作りの問題

2人組作りの問題の拡張として、3人組作りを考えます。ここで、3人組を作るための条件について、2通りの問題を考えることができます。

3人組作りの問題　3の倍数人の生徒がいるクラスで3人組を作る。どのような順番で3人組を作っても、最終的に誰もあぶれることがなく3人組を作り終えられるような交友関係は何か。

問題1 ただし、すべての2人について、その2人が友達か否かが指定されていて、3人組はどの2人も互いに友達である3人組であるときにのみ作れるものとする。
問題2 ただし、すべての3人について、その3人で組を作れるか否かが指定されているものとする。

問題1は、2人組作りの場合と同じように交友関係をグラフに表し、そこから三角形を除去していく操作を考えていけば良さそうです。おそらく完全グラフか正則完全三部グラフなら任意3人組作り可能でしょう。
しかし、問題1ではたとえば次のような状況が表現できません。

{A,B,C}、{A,B,D}、{A,C,D}では3人組が組める
{B,C,D}では3人組が組めない

たとえば、身長がある程度高い人が3人組の中に最低1人は必要で、B,C,Dの3人が全員低身長だったら、このような状況になるかもしれません。問題2の場合は、各3人に対して、その3人で組が作れるか否かをばっちりと指定してくれるので、この状況を表現することができます。しかし、この場合は通常のグラフでこの状況を表現することはできず、ハイパーグラフを用いて表現する必要があります。
これをトランプの言葉に直すと、スリーカード神経衰弱を考えることができますね。難しそう。

6.4. 参加者ごとにルールが違う神経衰弱

これは割と実用性がありそうな問題です。神経衰弱は参加者の記憶力に大きく依存するゲームなので、同じ人で何度かプレーする場合、勝敗が固定されがちです。そこで、参加者ごとのルールに差をつけることで、記憶力の良い人と悪い人が互角に戦えるようにする方法を考えたいです。
まずは参加者が2人の場合を考えましょう。参加者Aはグラフ $G_1=(V,E_1)$ に従って、参加者Bはグラフ $G_2=(V,E_2)$ に従ってカードを取っていきます。このとき、どのような順番でカードを取っていっても、最終的にすべてのカードを残すことなく取ることができるようなグラフ $G_1$ と $G_2$ の組はどのようなものでしょうか。また、適切なパワーバランスとなるようなルールはあるでしょうか。
たとえば、 $G_1$ が空グラフで $G_2$ が完全グラフという八百長ゲームは上の条件を満たします。おそらく、 $G=(V,E_1+E_2)$ が神経衰弱可能なグラフならば、上の条件を満たすと思います。

1本目の記事へのリンク
mel9.hatenadiary.com

2019-05-12

【ペア作りシリーズ①】「2人組作って〜」に誰もが安心できるクラスづくり

数学ペア作りシリーズ

0. ごあんない
1.「2人組作って～」にビクビクしたくない！
2.グラフの言葉に落とし込む
- 2.1.用語の紹介
- 2.2.元の問いをグラフの言葉で言うと？
3.交友関係が連結でない場合
4.交友関係は正則グラフでないといけないらしい
5.適切な友達の人数とは？
- 5.1.操作後のグラフが必ず連結にならなければいけないこと
- 5.2.操作後が連結かつ正則グラフになる場合
6.候補の絞り込みと十分性の証明
- 6.1. (2n-1)-正則グラフ
- 6.2. n-正則グラフ
7.交友関係の言葉に戻す

0. ごあんない

この記事はペア作りシリーズの一番はじめの記事です。
2番目の記事へのリンクはこちら。
mel9.hatenadiary.com

1.「2人組作って～」にビクビクしたくない！

今回は、2人組作って〜と言われたとき、どのような順番で2人組が作られていっても、全員があぶれることなく友達との2人組を組めるような交友関係はどのようなものになるのかを考えます。クラスの人数は偶数とします。

まず思いつくのは全員友達の仲良しクラスの場合です。この場合は誰もが誰とでも2人組を組むことができるので、誰もあぶれることはないですね。平和！

次に、初めから2人組が出来ている場合も考えられます。すなわち、全員友達が1人だけしかおらず、その友達としか2人組を組めないが、友達をほかの人に奪われることもないという状態です。2人組を作るのには適していますが、クラスとして成り立つかどうかには疑問が残る交友関係ですね......

この問いについて詳しくまとめると、

・クラスには偶数人の生徒がいるとする。
・クラス内のどの生徒の組も、友達同士であるか、友達ではないかのいずれかである。
・適当な順番で2人組を作っていく。1人が2つ以上の組に参加してはいけない。
・2人組は友達同士でしか組めない。

このとき、どんな順番で2人組が作られていったとしても、誰一人としてあぶれる人が出ないような交友関係はどのようなものだろうか？

という問いになります。

また、このような交友関係を任意2人組づくり可能な交友関係と呼ぶことにします(任意の順番で2人組づくりが可能であるという意味です)。

2.グラフの言葉に落とし込む

交友関係について調べるときは、交友関係をグラフに落とすと考えやすくなります。

たとえば、A,B,C,Dの4人がいて、AとB、AとC、AとD、BとC、CとDが友達であることを図1のグラフで表します。人を点で表し、人と人が友達であることを線で表す感じです。この線のことを辺と呼びます。

f:id:mel9:20190502031157p:plain:w150 — 図1

なお、このグラフが表す交友関係は、はじめにAとCが2人組を作ってしまった場合にBとDが2人組を組むことができないので、任意2人組作り可能ではありません。

2.1.用語の紹介

ここで、話をしやすくするために、グラフに関する用語を5つ紹介します。

連結なグラフ

グラフ上の任意の2点A,Bに対して、辺をたどってAからBまで行く道が存在するとき、そのグラフは連結であるといいます。具体的には、図1のグラフのようにひとかたまりになっているグラフは連結で、図2のグラフのように2つ以上のかたまりに分かれているグラフは非連結です。ここでいう「かたまり」のことをグラフの成分といいます。成分が1つだけなのが連結グラフで、2つ以上あるのが非連結グラフであるともいえます。
連結なグラフは、交友関係でいうと「クラスの誰からスタートしても、友達をたどっていくことで、クラスのすべての人にたどり着くことができる」ことに相当します。

f:id:mel9:20190502033127p:plain:w300 — 図2

点の次数

点につながっている辺の本数を、その点の次数といいます。図1のグラフではAの次数は3、Bの次数は2です。交友関係でいうと、友達の人数ですね。

正則なグラフ

グラフ上のすべての点の次数が等しいグラフを正則なグラフといいます。また、すべての点の次数がkであるとき、そのグラフをk-正則グラフといいます。たとえば、図3のグラフは2-正則グラフです。n人のクラスで全員仲良しの場合、全員が自分以外のn-1人と友達なので、交友関係は(n-1)-正則グラフということになります。

f:id:mel9:20190502032257p:plain:w150 — 図3

点の除去

グラフの中から1点を選んで、その点とその点につながっている辺をすべて取り除くことを、点を除去するといいます。図2のグラフから点Jを除去すると図4のようになります。

f:id:mel9:20190502034648p:plain:w300 — 図4

隣接

2つの点同士が辺で結ばれているとき、その2点は隣接していると言います。

2.2.元の問いをグラフの言葉で言うと？

友達同士で2人組を作ることは、グラフの言葉では次の操作に相当します。

操作　辺を1つ選び、その両端点を除去する。

元の問いをグラフの言葉に落とし込むと、次のようになります。

問　Gを偶数個の点を持つグラフとする。グラフに対する操作を次のように定める。

操作　辺を1つ選び、その両端点を除去する。

どのように操作を行ったとしても、全ての点を除去するまで操作を繰り返せるようなグラフGの条件を求めよ。

3.交友関係が連結でない場合

交友関係を表すグラフが連結でない場合について考えましょう。つまり、クラスが2つ以上のグループに完全に分離してしまっている場合を考えます。具体的には図2のグラフのような状況です。

このとき、グループαの人とグループβの人の間で2人組が作られることはないので、グループα、βのそれぞれが任意2人組づくり可能であれば、クラス全体が任意2人組づくり可能ということになります。したがって、グラフが非連結の場合は、それぞれのグループについて任意2人組づくり可能かを調べればよいことになります。

よって、ひとまず元の問題に

・交友関係を表すグラフは連結である。

という条件を加えて考えることにします。

問　Gを偶数個の点を持つ連結グラフとする。グラフに対する操作を次のように定める。

操作　辺を1つ選び、その両端点を除去する。

どのように操作を行ったとしても、全ての点を除去するまで操作を繰り返せるようなグラフGの条件を求めよ。

4.交友関係は正則グラフでないといけないらしい

この節がこの記事の核になります。

交友関係が任意2人組作り可能であるためには、交友関係のグラフが正則グラフであることが必要ということが示せます。

定理1
グラフGが連結で任意2人組作り可能であるならば、Gは正則グラフである。

このことを、グラフの点の個数に関する数学的帰納法で示します。つまり、

(I) 非正則で連結な2点のグラフは任意2人組作り可能ではない。

(II)非正則で連結な2k点以下のグラフが任意2人組作り可能ではないならば、非正則で連結な2k+2点のグラフは任意2人組作り可能ではない。

の2つを示すことになります。

(I)は、非正則で連結な2点のグラフは存在しないので真です。

(II)を示すために、次の定理2を示しましょう。

定理2
Gを偶数個の点を持つ非正則連結グラフとする。グラフGに対して、次の操作を行う。
操作　辺を1つ選び、その両端点を除去する。
このとき、うまく辺を選べば、操作後に残るグラフが次の(i)または(ii)を満たすようにできる。

(i) 正則でない成分をもつ。

(ii) 次数0の点をもつ。

4.1.定理2を利用した(II)の証明

定理2より、非正則で連結な2k+2点のグラフに対して、操作後に残る2k点のグラフが(i)または(ii)を満たすような操作を行うことができます。

操作が(i)を満たすときは、操作後に残るグラフのうち正則でない成分は、帰納法の仮定より任意2人組作り可能ではありません。したがって、元の2k+2点のグラフも任意2人組作り可能ではないことになります。操作が(ii)を満たすときは、次数0になった点が必ずあぶれるので、やはり任意2人組作り可能ではありません。

直感的な説明

任意2人組作り可能なためには、残り2人になった時点で図5のようなグラフ(1-正則グラフ)にならなければいけません。しかし、定理2が成り立つならば、最初のグラフが正則でない場合、正則でないことを維持し続けられるような操作が存在することになってしまいます。したがって、元のグラフは正則でなければなりません。

f:id:mel9:20190506225918p:plain:w150 — 図5

それでは、定理2を示していきましょう。
点の次数の最大値、最小値によって、5通りの場合分けになります。点の個数を2n、点の次数の最大値をt、最小値をsとします。場合分けは
(1) s=1の場合
(2) s=2かつt=2n-1の場合
(3) s=2n-2かつt=2n-1の場合
(4) 3≦s≦2n-3かつt=2n-1の場合
(5) s≧2かつt≦2n-2の場合
の5つです。
・連結　⇒　s≧1
・非正則　⇔　s≠t
であることと、n=1(点の個数が2個)の非正則連結グラフは存在しないので、
・n≧2(点は4個以上)
であることに注意します。

4.2.定理2の証明(1) 最小次数が1の場合

Gは連結なので、次数1の点は次数2以上の点に隣接していなければいけません。もし、次数1の点に隣接しているのが次数1の点だったすると、その2点でグラフが途切れてしまい、連結でなくなってしまうからです。このとき、次数1の点に隣接している点から伸びている辺のうち、次数1の点とを結ぶ辺以外の辺を選んで操作を行えば、次数1の点を孤立させることができます。下の図6でいうと、点A,Bを結ぶ辺を選んで除去すれば良いです。この操作が条件(ii)「操作後のグラフが次数0の点を持つ」を満たす操作になります。
交友関係でいうと、友達が1人しかいない人がいたら、その人を孤立させることができるということになります。厳しいですね。

f:id:mel9:20190506233521p:plain:w200 — 図6

4.3.定理2の証明(2) 最小次数が2で、最大次数が2n-1の場合

次数が2n-1の点はすべての点と隣接していることがポイントになります。次数2の点に隣接している点のうち、片方は次数2n-1の点ということになります。もう片方を点Aと呼ぶと、次数2n-1の点はこの点Aとも隣接していることになります。ここで、点Aと次数2n-1の点を除去すれば、次数2の点が孤立します。
交友関係でいうと、全員と友達の人がいれば、友達が2人いる人であっても孤立させることができるということになります。2人しかいない友達が早々に2人組を作ってしまったときの絶望感は想像したくないですね。

f:id:mel9:20190506235228p:plain:w200 — 図7

4.4.定理2の証明(3) 最小次数が2n-2で、最大次数が2n-1の場合

握手補題を利用します。

握手補題
次数が奇数であるような点の個数は偶数個である。

グラフの中で辺が1本増えるごとに、点の次数の総和は2増えます。つまり、次数の総和は必ず偶数でなければいけません。ここで仮にグラフ内に次数が奇数であるような点が奇数個あるとするならば、次数の総和が奇数になってしまいます。したがって、次数が奇数であるような点の個数は必ず偶数個になります。パーティ会場で参加者同士が適当に握手をしたとき、奇数人と握手をした人数は必ず偶数人になっているということです。
このグラフでは点の次数は2n-1または2n-2のどちらかなので、次数が2n-1の点の個数が偶数個であることが言えます。次数が2n-2の点の個数も偶数個です。
ここで、次数2n-2の点が2個の場合と4個以上ある場合で場合分けをします。

4.4.1.次数2n-2の点が2個の場合

次数2n-1の点をどれでもいいから2つ選んで除去する操作が、定理2の条件(i)「操作後のグラフが正則でない成分を持つ」または(ii)「操作後のグラフが孤立点を持つ」を満たす操作になります。n=2なら、次数2n-2(=2)の点がそろって孤立します(図8参照)。n≧3の場合は、次数2n-1の点のうち除去されなかったものは次数が2n-3になり、次数2n-2だった点の次数は2n-4になります。この2点は操作後も隣接しているので、この2点を含む成分が非正則な連結成分になります。

f:id:mel9:20190507001438p:plain:w200 — 図8

4.4.2.次数2n-2の点が4個以上の場合

この場合、次数2n-2の点同士が隣接している部分が必ずあります。そのような部分に着目しましょう(図9)。図9中の赤い辺(次数2n-1の点と2n-2の点を結ぶ辺)を選んで操作を行います。すると、図中に残された点のうち、次数2n-1だった方は次数2n-3に、次数2n-2だった方は次数2n-4になります。この2点は操作後も隣接しているので、この2点を含む成分が非正則な連結成分になります。

f:id:mel9:20190507002207p:plain:w200 — 図9

4.5.定理2の証明(4) 最小次数が3以上2n-3以下で、最大次数が2n-1の場合

次数sの点には次数2n-1の点が必ず隣接しています。これとは別に次数sの点に隣接している点を点Aとします。点Aにも次数2n-1の点が隣接していますが、点Aの次数は3以上なので、次数sの点、次数2n-1の点とは別に点Aに隣接している点があります。それを点Bとします。点Bと次数sの点が隣接しているか否かは問いません。ここで点Aと点Bを結ぶ辺を選んで操作を行います。すると、次数2n-1の点の次数は2n-3に、次数sの点の次数はs-1かs-2になります。2n-3>s-1なので、操作後もこの2点の次数は異なります。操作後もこの2点は隣接したままなので、この2点を含む成分が非正則な連結成分になります。

f:id:mel9:20190507002726p:plain:w200 — 図10

4.6.定理2の証明(5) 最小次数が2以上で、最大次数が2n-2以下の場合

ここが本丸です。ここでは、定理2の対偶となる次の補題1を証明します。

補題1
Gを2n個の点を持つ連結グラフとする。また、Gの全ての点は次数が2以上2n-2以下であるとする。グラフGに対して、次の操作を行う。
操作　辺を1つ選び、その両端点を除去する。
このとき、操作後に残るグラフが次の(i)または(ii)を満たすような辺の選び方が存在しないならば、Gは正則グラフである。
(i) 正則でない成分をもつ。
(ii) 次数0の点をもつ。

方針としては、次数がtの点から出発して、Gのすべての点の次数がtになることを示すことになります。
次数tの点の一つを点Aとします。t≦2n-2より、点Aには隣接していない点があります。これを点Bとします。すると、点Bに隣接している点の次数がtであることが証明できます。これを利用して、点B(点Aに隣接していない点)の次数もtであることが証明できます。最後に、点Aに隣接している点の次数がtで有ることを証明します。グラフ上の点は点Aに隣接しているかしていないかのいずれかであるので、これで証明完了です。

目次
4.6.1. 点Aに隣接していない点に隣接している点の次数はt
4.6.2. 点Aに隣接していない点の次数はt
4.6.3. 点Aに隣接している点の次数はt
4.6.4. 補題1の証明

4.6.1. 点Aに隣接していない点に隣接している点の次数はt

この節では次の補題2を証明します。主張の内容は、補題1の条件下では、最大次数の点に隣接していない点に隣接している点の次数も最大次数になるということです。

補題2
Gを2n個の点を持つ連結グラフとする。また、Gの全ての点は次数が2以上2n-2以下であるとする。Gの最大次数をtとする。グラフGに対して、次の操作を行う。
操作　辺を1つ選び、その両端点を除去する。
このとき、操作後に残るグラフが次の(i)または(ii)を満たすような辺の選び方が存在しないならば、次数tの点に隣接していない点に隣接している点の次数はtである。
(i) 正則でない成分をもつ。
(ii) 次数0の点をもつ。

点Aの次数をtとし、点Bを点Aに隣接していない点とします。グラフは連結なので点Aから点Bに向かう道があります。この道上にあって、点Bに隣接している点を点Cとし、点Cの次数をcとします。図11を参考にしてください。なお、図中の辺ACが緑色になっているのは、点Aと点Cの間に本当に辺があるとは限らないが、点Aから点Cに行く点Bを通らない道があることを表しています。また、破線は隣接していないことを表しています。

f:id:mel9:20190512021952p:plain:w200 — 図11

ここで、点Bの次数は2以上ですので、点C以外にも点Bに隣接している点があります。その中から1つを選んで点Dとし、点Dの次数をdとします。
ここで辺BDを選んで操作を行うと、操作後にもAとCは同じ成分内にあって、点Aの次数はtかt-1、点Cの次数はc-1かc-2になります。したがって、Aは最大次数の点なので、操作後のグラフが正則でない成分を持たないようにするためには、操作前のグラフはc=tかつ、AとDが隣接しているかつ、CとDが隣接していない状況でなければいけません(図12)。

f:id:mel9:20190512022012p:plain:w200 — 図12

ここで辺BCを選んで操作を行うと、操作後にもAとDは同じ成分内にあって、点Aの次数はtかt-1、点Dの次数はd-1になります。したがって、操作後のグラフが正則でない成分を持たないようにするためには、操作前のグラフはd=tかつ、AとCが隣接している状況でなければなりません。
A、B、Cを固定して、Bに隣接している点Dの選び方を自由に取り換えて上の議論を続ければ、点Bに隣接している点の次数はすべてtでなければならないことがわかります。

4.6.2. 点Aに隣接していない点の次数はt

上の補題2の証明中で、元のグラフ中で点Cと点Dは隣接していないことが示されました。ここで次数がtである点Cとそれに隣接していない点である点Dに対して補題2を適用すると、点Dに隣接する点Bの次数はtということになります。

4.6.3. 点Aに隣接している点の次数はt

次数がtである点Bとそれに隣接していない点である点Aに対して補題2を適用すると、点Aに隣接する点の次数はtということになります。

4.6.4. 補題1の証明

グラフG上の点は点Aに隣接しているかしていないかのいずれかであるので、4.6.2.および3.節によって、Gのすべての点の次数がtであることが示されました。
したがって、Gは正則グラフです。

以上により、交友関係が任意2人組作り可能であるためには、交友関係のグラフが正則グラフであることが必要であることが示されました！
平和に2人組作りを終えるためには、クラスのみんなが足並みをそろえて友達の人数が同じでなければいけないようです。

5.適切な友達の人数とは？

4節で、任意2人組作り可能なグラフの候補が正則グラフに絞られました。
では、友達の人数は何人であれば良いのでしょうか？
たとえ元の交友関係を表すグラフが正則グラフであったとしても、操作後に残るグラフが(i)「正則でない成分をもつ」または(ii)「次数0の点を持つ」を満たしてしまうことがあるようなグラフでは、2人組を作り終えることができません。つまり、ここで考えなければいけないのは次の問題です。

問　Gを偶数個の点を持つ連結なk-正則グラフとする。グラフに対する操作を次のように定める。

操作　辺を1つ選び、その両端点を除去する。

操作後に残るグラフが次の(i)または(ii)を満たすような辺の選び方が存在しないための、Gの条件を求めよ。
(i) 正則でない成分をもつ。
(ii) 次数0の点をもつ。

ここで注意したいのは、操作後に残るグラフの点の次数はk、k-1、k-2のどれかであるということです。除去される点は2つなので、点の次数は高々2までしか減りません。

5.1.操作後のグラフが必ず連結にならなければいけないこと

この節では、操作後に残ったグラフが非連結になったならば、そのグラフは条件(i)「正則でない成分をもつ」または(ii)「次数0の点を持つ」を満たしてしまうことを証明します。
背理法で証明します。操作後のグラフが非連結になり、かつ、そのグラフが条件(i)も(ii)も満たさない(孤立点がなく、操作後のグラフの各成分は正則)と仮定します。操作後のグラフの各成分のうち、少なくとも1点は除去された点の少なくとも一方と隣接していました。したがって、操作後のグラフの各成分が正則な成分であるなら、その成分の各点の次数はk-1かk-2になります。すなわち仮定より、操作後のグラフに次数kの点は存在せず、次数はk-1かk-2のいずれかということになります。
次数k-1の点の個数をm個とします。(k-1)-正則な成分にはk個以上の点が必要なので、m≧kが必要です。同じく、2n-2-m≧k-1が必要です。
ここで、グラフの辺の本数について考察してみましょう。辺が1本増えるごとに次数が2増えるので、グラフの辺の本数は次数の総和÷2です。よって、操作前のグラフの辺の本数は2n×k÷2=nk本です。対して、操作によってなくなる辺の本数は、次のように考えることで、2k-1本であることがわかります。除去される2つの点からはそれぞれk本の辺が伸びているので合計2k本、これでは除去される2つの点同士を結ぶ辺を二重にカウントしてしまっているので1を引いて2k-1本です。したがって、操作後に残るグラフの辺の本数はnk-2k+1本になります。
これを利用して、操作後のグラフの辺の本数に関して式を立てます。

$m(k-1)+(2n-2-m)(k-2)=2(nk-2k+1)$

これを解くと、mをnとkで表せます。m≧kと合わせると次のようになります。

$m=4n-2k-2\geq k$

同じく、2n-2-m≧k-1を用いると次の不等式が得られます。

$2n-2-m=-2n+2k\geq k-1$

この2つの不等式を合わせると、次のような不等式になります

$3k+2\leq 4n\leq 2k+2$

kは正なので、この不等式は偽です。したがって、仮定が誤りで、操作後のグラフが非連結になったならば、そのグラフは条件(i)「正則でない成分をもつ」または(ii)「次数0の点を持つ」を満たします。
この結果は、「グラフが任意2人組作り可能であるためには、操作後のグラフが必ず連結になるようなグラフでなければならない」ことを表しています。また、4節の結果より、任意2人組作り可能なグラフは操作後に残るグラフの連結成分がすべて正則でなければいけませんから、グラフが任意2人組作り可能であるためには、操作後のグラフが必ず連結かつ正則になるようなグラフでなければならないことになります。

5.2.操作後が連結かつ正則グラフになる場合

5.1.節で述べたように、操作後に残るグラフの辺の本数はnk-2k+1です。さらに、操作後に残るグラフは2n-2点の(k-2)-正則連結グラフか(k-1)-正則連結グラフにならなければいけません。ここから、辺の本数に関する式を立てて、kをnで表すと、

$2(nk-2k+1)=(k-2)(2n-2) \Leftrightarrow k=2n-1 \\ 2(nk-2k+1)=(k-1)(2n-2) \Leftrightarrow k=n$

ですので、操作後のグラフが(k-2)-正則連結グラフになるにはk=2n-1が必要であり、(k-1)-正則連結グラフになるにはk=nが必要です。すなわち、任意2人組作り可能なグラフの候補は以下の2通りしかないことがわかります。
・(2n-1)-正則グラフで、操作後には必ず(2n-3)-正則連結グラフになる。
・n-正則グラフで、操作後には必ず(n-1)-正則連結グラフになる。

6.候補の絞り込みと十分性の証明

6.1. (2n-1)-正則グラフ

すべての点の次数が2n-1になるためには、すべての点が自分以外のすべての点と隣接していなければいけません。したがって、単に(2n-1)-正則グラフと言っただけで、グラフの形は一意に決まります。この(2n-1)-正則グラフのことを完全グラフと呼びます。交友関係が完全グラフであるということは、みんな友達の平和なクラスであることを意味しているので、当然任意2人組作り可能です。

6.2. n-正則グラフ

(2n-1)-正則グラフの場合と違って、単にn-正則グラフと言ってもグラフの形は一意には決まりません。まず、n-正則グラフで、操作後には必ず(n-1)-正則グラフになるグラフがどのような形のグラフなのか調べましょう。
操作後に残った点の次数がすべて1ずつ減っているということは、操作によって除去された2点の両方に隣接していた点は存在せず、2点のいずれにも隣接していなかった点も存在しません。除去する辺をAB、Aに隣接している点の集合をβ、Bに隣接している点の集合をαとしましょう(図13)。Cをαの元、Dをβの元とします。ここでBCの除去を考えると、操作後のグラフが(n-1)-正則グラフになるためには、Cはβに属するすべての点と隣接していなければならないことがわかります。同じくADの除去を考えると、Dはαに属するすべての点と隣接していなければならないことがわかります。したがって、このグラフはAおよびαに属するすべての点が、Bおよびβに属するすべての点と隣接しており、かつ、Aおよびα内、Bおよびβ内には隣接している点の組み合わせはないようなグラフになります。

f:id:mel9:20190512040903p:plain:w150 — 図13

このように、点集合を2つに分割して、一方の点集合に属するすべての点からもう一方の点集合に属するすべての点に向かって辺が伸びており、かつ、各集合内の点の間には辺が無いようにできるグラフのことを、完全二部グラフと言います。
n-正則グラフで、操作後には必ず(n-1)-正則グラフになるグラフは、n-正則完全二部グラフでなければいけません。
逆に、n-正則完全二部グラフは任意2人組作り可能であることを説明します。
数学的帰納法を用います。まず、1-正則完全二部グラフは下の図5のようなグラフなので、任意2人組作り可能です。

n-正則完全二部グラフの点集合を上の条件を満たすように2つの点集合に分割し、それぞれα、βとします。このグラフに対して操作を行うと、αから1点、βから1点が除去され、残されたグラフは(n-1)-正則完全二部グラフとなります。帰納法の仮定より(n-1)-正則完全二部グラフは任意2人組作り可能であるので、n-正則完全二部グラフもやはり任意2人組作り可能です。

7.交友関係の言葉に戻す

長い道のりでしたが、任意2人組作り可能な連結グラフは完全グラフと正則完全二部グラフの2通りに限られることが示されました！
完全グラフはみんな友達！なクラスです。対して、正則完全二部グラフは全員がクラスの半数と友達ですが、友達の友達は誰一人として友達ではないクラスです。このクラスでは共通の友達を持つ友達は一人もいません。「この前、友達の○○がさ～」って話を振ると、必ず「そいつ友達じゃないわ」と返ってきます。このクラスで3人以上の組を作ろうとすると詰みます。
さて、3節でクラスの交友関係が非連結の場合を除外したのを思い出しましょう。この2通りだけではなく、クラスの交友関係が偶数人の完全グラフや正則完全二部グラフの和になっている場合も、クラス全体が任意2人組作り可能な交友関係になります。というわけで、
誰一人として「2人組作って〜」に怯えることなく過ごすために、クラスの交友関係を完全グラフか正則完全二部グラフ(か、その和)にしましょう！

ここまで閲覧ありがとうございました。

この記事の続きはこちら
mel9.hatenadiary.com

2018-12-03

Baltic Way 2018を勝手に解いた感想

先日、Baltic Way 2018の問題を解きました。

Baltic Wayとは、毎年11月にバルト海沿岸の国・地域で行われている高校生向け数学コンテストです。制限時間4時間半の間に、20問の問題を1チーム5人で協力して解くという形式です。問題の難易度や質は様々なので、問題の取捨選択が重要となります。
本物に準じて解こうと思いましたが、1人が寝坊したため4人×5時間+1人×1時間半で解答しました。

今年度の問題は以下のURLから入手できます(Baltic Wayの公式ページ。日本語版はもちろんありませんが......)

http://www.pdmi.ras.ru/EIMI/2018/Baltic_way/index.html

以下、1番から順に雑に感想を記します。ネタバレに注意。

個人的に、ネタバレをされると特にもったいないと思うのは4番と6番です。解答を見る前に是非どうぞ。問題の和訳に自信がないので、誤りがあれば指摘お願いします。

　Problem 4　次の式が任意の自然数 $k$ と実数列 $x_1,\ldots,x_k$ に対して成り立つような関数 $f:[0, \infty )\to [0,\infty )$ を全て求めよ。

$f(x_1^2 + \cdots +x_k^2)=f(x_1)^2+\cdots f(x_k)^2$

　Problem 6　 $n$ を正の整数とする。エルフが $\mathbb{R}^3$ の格子点上を動く。エルフははじめ原点にいる。移動する際には、今いる点からちょうど $\sqrt{n}$ だけ離れた点にのみ移動できる。移動するのは大変なので、エルフは偶数回目の移動後にはnormalな状態だが、奇数回目の移動後にはstrangeな状態になってしまう。エルフが移動を繰り返すことで、全ての格子点にnormalな状態で到達することができるような $n$ を全て求めよ。

3番

問題用紙を一目見ると目に入る、いかつい不等式問題。見るからに難しそうなので後回しでしたが、3時間半くらい経った頃に考え始めた参加者がいました。問題を易しくした、

$\displaystyle\frac{1}{\sqrt{a+3}}+\frac{1}{\sqrt{b+3}}\leq 1$

という不等式から拡張できないかということも考えられましたが、解答できませんでした。終了後に大会の結果を見ると、出場した全チームがこの問題に答えられていない難問でした。

4番

関数方程式の問題。序盤に、xが有理数の範囲ではf(x)=0かf(x)=xに限られること、fが微分可能であればその2つに決定することが示されましたが、その後4時間進展がなく、解答できませんでした。この条件式からfが微分可能であることを導くのは難しそう。
模範解答では、無理数の場合は有理数の場合から不等式評価する方針をとっています。つまり、固定された無理数xに対して、xより大きい有理数rについてはf(x)≦f(r)であることと、xより小さい有理数rについてはf(x)≧f(r)であることを示すことで、f(x)=0,xであることを示すやり方です。

5番

面白い問題でした。「fがgeneratingであること」と「φ(x)=xに対してg_1,......,g_kが存在すること」が同値であることにすら気づけなかったのは残念でした。

6番

これはチェスをよくする人なら思いつきやすかったりするのかな？解答を見ると、格子点を市松模様に塗るというアイデアが出るか出ないかが勝負の問題でしたが、考え始めたのが遅かったのもあって思いつくことができませんでした。
ちょっと難しめのパズル問題として面白い問題でした。

8番

証明しなければならないことが特殊で面食らいました。解答を見ると大したことないように見えますが、こういう問題は何をすればいいのか戸惑います。

9番

解けた問題の一つです。大会の結果を見ると点数を引かれているチームが多いですが、少なくとも3点、まあ4点は入る答案を書けた気がします(5点満点)。
証明は2パートに分かれていて、「Olgaが負けることはないこと」「ゲームが無限に続くことはないこと」の2つを示す必要があります。前者はトイレに行っている間に、後者は他の参加者に問題の内容を話している最中に思いつきました。歩いたり、人と話したりすることは大事ですね。

10番

20問の中では群を抜いて易しい問題でした。問題としてもあまり面白くはないかなあ。

11番

幾何と思わせておいて整数の問題。幾何嫌いの参加者が多かったので幾何は放置されがちでしたが、この問題が唯一まともに取り組まれ、解答されました。aとcが互いに素であるという条件をどう使うかがわからず、私自身は30分ほど考えて他の人に投げました。

16番

一番最初に解かれました。すごい。私は解答の査読をしました。

17番,19番,20番

いつの間にか解かれてました。すごい。

18番

フェルマーの小定理を利用したあとの手が浮かばず、ドツボに嵌ってしまった参加者がいました。私も20分くらい溶かしました。模範解答はたった5行で脱力ものです。

2017-08-31

検査陽性のパラドックスと再検査

検査陽性のパラドックスについて。

まずはこちらをどうぞ。

問1　ある国には $10^{16}$ 人の人が住んでいる。この国にはXという病気が流行していて、国民は $10^{-6}$ の割合( $10^{6}$ 人に1人の割合)でXに感染しているという。
また、Xという病気に感染しているかどうかを判定する簡易検査キットYがある。このキットを使用したとき、本当に感染している人に対して陽性と診断する確率(感度)と、本当に感染していない人に対して陰性と診断する確率(特異度)は、ともに $1-10^{-3}$ (99.9%)である。
Aさんが検査キットYで検査をしたとき、陽性と診断が出た。このとき、AさんがXに感染している確率(陽性反応的中度)を求めよ。

$10^{16}$ 人(1京人)も住んでいる国がどこにあるんだとか、そういうところには目を瞑ってください。

実際のところ、この国にいてXに感染している人は $10^{10}$ 人です。
そのうち、陽性が出る人は $10^{10}-10^{7}$ 人。まあおよそ $10^{10}$ にしちゃいましょう。
陰性が出るのは $10^{7}$ 人ですね。
同様に、実際のところXに感染していない人についても考えてみると、陰性が出る人は $10^{16}$ 人、陽性が出る人は $10^{13}$ 人になります。
まとめると以下の表のようになります。

Aさんは陽性が出ましたが、陽性が出た約 $10^{13}$ 人のうち、本当に陽性なのは約 $10^{10}$ 人。つまり、Aさんが本当にXに感染している確率(陽性反応的中度)は約 $10^{-3}$ です。

感度と特異度が99.9%という数値なのに対し、陽性反応的中度は0.1%とかなり低くなってしまうのが、「直感とは違う」という意味で「パラドックス」と呼ばれる所以です。
このようなパラドックスが生まれる原因となるのは、Xの感染率が、感度や特異度に比べて小さいことにあります。

一般的な検査陽性パラドックスはここで終わりですが、この記事ではさらに次を見てみましょう。

問2　陽性反応が出たAさんがもう一度検査キットYで検査をしたとき、再び陽性と診断が出た。このとき、AさんがXに感染している確率を求めよ。

再検査をしてみました。これで確率はどう動くでしょうか。

実際に感染している人のうち、2回連続で陽性反応が出る人数は、 $10^{10}\times (1-10^{-3})\times (1-10^{-3})$ で、約 $10^{10}$ 人。
実際は感染していない人のうち、2回連続で陽性反応が出る人数は、 $10^{16}\times 10^{-3}\times 10^{-3}$ で、約 $10^{10}$ 人です。

したがって、Aさんはこの約 $2\times 10^{10}$ 人のうちの1人ですので、実際にXに感染している確率は約50%です。

こうなると、かなり現実味を帯びた数字になります。
Aさんのおかれた状況をまとめると、

まだ1回も検査を受けていない状態……感染率 $10^{-6}$
1回検査を受けて、陽性が出た状態……感染率 $10^{-3}$
2回検査を受けて、2回とも陽性が出た状態……感染率 $\displaystyle\frac{1}{2}$

となります。微妙な言い方ですが、1回の検査はおよそ $10^{3}$ スケールで的中率を上昇させるという結論になりそうです(この実験では数字を丸めまくってるので、回数を重ねるほど誤差が生じますが)。

1回では的中率が低かった検査も、2回の検査をすると的中率が大幅に上昇する可能性があることがわかります。
感度、特異度がともに99.9%の検査をやっても陽性反応的中度は0.1%しかない！ってのも直感に反しますが、陽性反応的中度が0.1%の検査を2回やると的中度は50%！ってのも、うーんって感じがします。

2016-09-18

和積公式の作図

数学高校数学

前回の記事では、ふつう和積公式で解くような問題を、様々な解法で解きました(まだご覧でない方は是非ご覧ください)。

mel9.hatenadiary.com

今回は解法4の図をもとに、和積公式を作図で確かめたいと思います。紙とペン、定規とコンパスを用意して、実際に追ってみてください。

確かめるのは $\cos \alpha +\cos \beta =2\cos \frac{\alpha +\beta }{2} \cos \frac {\alpha -\beta }{2}$ で、 $0^\circ < \alpha < 90^\circ ,0^\circ < \beta < 90^\circ$ とします。

0.準備

①円 $Ｏ$ を描き、直径 $AB$ をひく
② $\angle AOX =\alpha ,\angle BOY =\beta$ となる2点 $X,Y$ を、 $AB$ に関して同じ側にとる

f:id:mel9:20160917171455p:plain

まずは円 $Ｏ$ を半径1の単位円としてしまいましょう。
図では垂線が下りていますが、垂線の足を結んだ線分の長さが $\cos \alpha +\cos \beta$ となります。

1. $\cos \frac{\alpha +\beta }{2}, \cos \frac {\alpha -\beta }{2}$ をつくる

③ $\angle XOY$ の二等分線を引き、円 $Ｏ$ との交点のうち直線 $AB$ に関して $X$ と同じ側にあるものを点 $P$ とする
④ $P$ から $OY$ に垂線を下ろし、足を点 $H$ とする
⑤直線 $OB$ に関して $Y$ に対称な点 $Y'$ をとる
⑥ $\angle XOY'$ の二等分線を引き、円 $Ｏ$ との交点のうち直線 $AB$ に関して $X$ と同じ側にあるものを点 $Q$ とする
⑦ $Q$ から $OY'$ に垂線を下ろし、足を点 $I$ とする

f:id:mel9:20160918175244p:plain

$\angle XOY$ , $\angle XOY'$ はそれぞれ $180^\circ -(\alpha +\beta ) ,180^\circ -(\alpha -\beta )$ となります。
$\angle POY$ , $\angle QOY'$ がその半分の大きさの角となり、 $PO=1,QO=1$ ですから、 $PH=\sin \frac{180^\circ -(\alpha +\beta) }{2}, QI=\sin \frac {180^\circ -(\alpha -\beta) }{2}$ となります。
したがって $PH=\cos \frac{\alpha +\beta }{2}, QI=\cos \frac {\alpha -\beta }{2}$ です。

2. $\cos \frac{\alpha +\beta }{2}, \cos \frac {\alpha -\beta }{2}$ 同士を掛け合わせる

⑧ $O'A'=OA,O'H'=PH$ となる3点O',H',A'を、同一直線上にこの順にとる(とれる)
⑨ $A'Q'=QI$ となる点 $Q'$ を直線 $O'A'$ 外にとる
⑩ $H'$ を通り $A'Q'$ と平行な直線をひく
⑪ $O'Q'$ と⑩の交点を $M'$ とする

f:id:mel9:20160918175251p:plain

新しいフィールドで、比を用いて線分のかけ算を行います。
$O'A'=1$ なので、 $O'A':O'H'=A'Q':M'H'$ より、 $M'H'=O'H'\times A'Q'$ です
よって1の最後の式より、 $M'H'=\cos \frac{\alpha +\beta }{2} \cos \frac {\alpha -\beta }{2}$ となります

3. $\frac{1}{2}(\cos \alpha +\cos \beta )$ との一致を確認する

⑫点 $X,Y$ から直線 $AB$ におろした垂線の足をそれぞれ点 $S,T$ とする
⑬線分STの中点をとり、点 $M$ とする
⑭コンパスで $SM=M'H'$ を確認する

f:id:mel9:20160918175255p:plain

ここまで来ればあとは確認だけです。最後に綺麗に一致したときはなかなか感動します。実際に描いてみたのが以下の写真です。

f:id:mel9:20160918191607j:plain
f:id:mel9:20160918191611j:plain

実際に描いてみると、円Ｏを利用することで、コンパスを使う回数をかなり節約できることが分かりますね。基本作図を殆ど使っているのでその確認がてら一回やってみては如何でしょうか。

2016-09-11

cos40°+cos80°+cos160°の値の求め方5通り

数学高校数学

スタンダードに和積公式を用いる

2倍してから和積公式を用いる

3倍角の公式を用いる

幾何的に解く(個人的に一番好き)

2倍角の公式を用いる

2018年8月17日　少しリニューアルしました。
ちょっと質の悪い解法2つを削除して、新たに解法5を追加しました。

1. 和積公式による解法

高校数学の問題集に載っているとすればこの解法でしょう。

用いる和積公式は $\cos A + \cos B=2\cos \frac{A+B}{2} \cos \frac{A-B}{2}$ です。

$\begin{eqnarray*} \cos40^\circ+\cos80^\circ+\cos160^\circ &=& \cos40^\circ+2\cos120^\circ \cos40^\circ \\ &=& \cos40^\circ(1+2\cos120^\circ) \\ &=& 0 \end{eqnarray*}$

よって答えは $0$ となります。

2. 2倍してから和積公式を用いる解法

1つめの解法は一般的な解法ですが、こちらの方がちょっとエレガントです。

$2(\cos40^\circ+\cos80^\circ+\cos160^\circ ) \\ =(\cos40^\circ+\cos80^\circ )+(\cos80^\circ+\cos160^\circ )+(\cos40^\circ+\cos160^\circ ) \\ =2\cos20^\circ\cos60^\circ+2\cos40^\circ\cos120^\circ+2\cos60^\circ\cos100^\circ \\ =-\cos160^\circ-\cos40^\circ-\cos80^\circ \\ =-(\cos40^\circ+\cos80^\circ+\cos160^\circ)$

$2$ 倍して自身の $-1$ 倍に一致したので $\cos40^\circ+\cos80^\circ+\cos160^\circ$ は $0$ になります。

3. 3倍角の公式を用いる解法

$40^\circ ,80^\circ ,160^\circ$ という角だからこそ、この解法がハマります。
それぞれの角を $3$ 倍するとcosの値が一致するような角になるので、それを利用します。

$\begin{eqnarray*} 4\cos^3 40^\circ-3\cos40^\circ&=&\cos120^\circ=-\frac{1}{2} \\ 4\cos^3 80^\circ-3\cos80^\circ&=&\cos240^\circ=-\frac{1}{2} \\ 4\cos^3 160^\circ-3\cos160^\circ&=&\cos480^\circ=-\frac{1}{2} \\ \end{eqnarray*}$
より、 $4x^3-3x+\frac{1}{2}=0$ という方程式を考えます。
すると、 $\cos40^\circ,\cos80^\circ,\cos160^\circ$ は相異なる三数であるので、先の方程式の三解に一致します。
求めるのは三解の和なので、解と係数の関係により答えは $0$ となります。

ただのcosの和に解と係数の関係を用いるのは面白いです。副産物として $\displaystyle\cos40^\circ \cos80^\circ \cos160^\circ =-\frac{1}{8}$ も求まりました。

4. 幾何的な解法

f:id:mel9:20160911040557p:plain
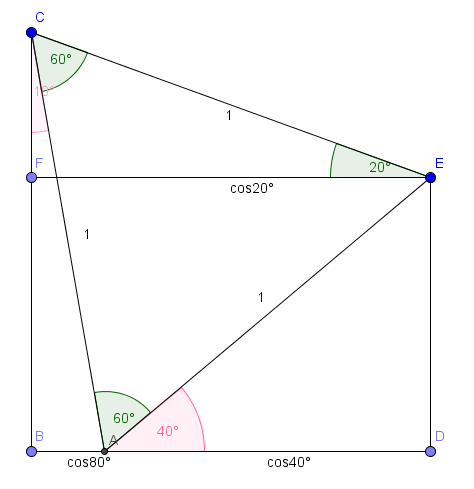
この解法がこの5つの中で最も綺麗だと思います。僕はこれが一番好きです。
3点 $\rm B,A,D$ を一直線上に並べ、 $\rm BA=\cos80^\circ,AD=\cos40^\circ$ とします。
ここで2点 $\rm C,E$ を、 $\rm \angle BAC=80^\circ, \angle DAE=40^\circ, \angle CBA=\angle EDA=90^\circ$ を満たすように、直線 $\rm BD$ に関して同じ側にとると、 $\rm AC=CE=1$ となります。
$\rm\angle CAE=60^\circ$ なので、 $\rm\triangle CAE$ は正三角形です。
よって $\rm\angle BCE=70^\circ$ なので、直線 $\rm BC$ 上の点 $\rm F$ を $\rm\angle EFC=90^\circ$ となるようにとると、 $\rm\angle CEF=20^\circ$ 。
したがって、 $\rm EF=\cos20^\circ$ となります。
$\rm EF=BA+AD$ なので、 $\cos40^\circ+\cos80^\circ-\cos20^\circ=0$ 。
すなわち、 $\cos40^\circ+\cos80^\circ+\cos160^\circ$ も $0$ です。

正三角形がうまくはまってくれるのが綺麗ですね。

5. 2倍角の公式を用いる解法

$\cos80^\circ, \cos160^\circ$ に倍角の公式を用いて $\cos40^\circ$ に帰着させます。 $\cos40^\circ$ はどうにもならないと思いきや、救世主が現れてなんとかなります。
$\begin{eqnarray*} \cos40^\circ+\cos80^\circ+\cos160^\circ &=& \cos40^\circ+2\cos^240^\circ -1+2\cos^280^\circ-1 \\ &=& \cos40^\circ+2\cos^240^\circ +2(2\cos^240^\circ -1)^2-2 \\ &=& 8\cos^440^\circ -6\cos^240^\circ +\cos40^\circ \\ &=& \cos40^\circ ( 2(4\cos^340^\circ -3\cos40^\circ ) +1) \\ &=& \cos40^\circ ( 2\cos120^\circ +1) \\ &=& 0 \end{eqnarray*}$
5つめの式から6つめの式に移るときに3倍角の公式を利用しています。

ところで、元の問題の角が $40^\circ ,80^\circ ,160^\circ$ の代わりに $80^\circ ,160^\circ ,320^\circ$ であっても、この5つめの解法の式変形はすべて行えます。 $\cos(40\times 3)^\circ = \cos(80\times 3)^\circ$ が成り立つからです。したがって、 $\cos80^\circ+\cos160^\circ+\cos320^\circ$ も $0$ になります。これは $\cos40^\circ = \cos320^\circ$ とも整合性が取れています。
ここら辺をよく考えると、 $40^\circ$ という角がうまくいく理由が見えてきて、他のきれいな式変形が可能な角を探し当てることができるかもしれませんね。

5つの解法を見つけた順番は、3→2→4→1→5でした。1番が見つかったときは脱力しました。

問題

制約

解説

0.ごあんない

1.「任意2人組作り可能」を別の意味に解釈する

1.1.神経衰弱可能

1.2.ババ抜き可能とジジ抜き可能

1.3.この記事の目標

1.4.グラフの言葉への書き換え

2.非連結の場合

2.1.ババ抜き可能なグラフはジジ抜き可能

2.1.1.連結成分が1個の場合

2.1.2.連結成分がn個の場合

2.2.奇数点完全グラフ2個の和はジジ抜き可能

2.3.それ以外の非連結グラフはジジ抜き不可能

2.3.1.連結成分が3個以上で、奇数点の成分が2個以上含まれるとき

2.3.2.奇数点の成分が含まれないとき

2.3.3.連結成分が2個で、両方とも奇数点のとき

3.連結グラフに関する考察の方針

3.1.独立集合の大きさが高々2であるグラフはジジ抜き可能

3.2.完全マッチングを使った問題の言い換え

3.3.ジジ抜き不可能の再帰的な言い換え

4.連結の場合

4.1.グラフが6点の場合

4.2. 2つの独立集合以外に3点以上の独立集合をもたない二部グラフはジジ抜き可能

4.3. 2つの独立集合以外に3点以上の独立集合をもたない二部グラフであることと同値な条件

4.4. 帰納法を回す

5.結論

6.今後の展望

6.1. ババ抜き可能やジジ抜き可能のさらなる別解釈

6.2. 欠席者と先生付きの2人組作りの問題

6.3. 3人組作りの問題

6.4. 参加者ごとにルールが違う神経衰弱

0. ごあんない

1.「2人組作って～」にビクビクしたくない！

2.グラフの言葉に落とし込む

2.1.用語の紹介

連結なグラフ

点の次数

正則なグラフ

点の除去

隣接

2.2.元の問いをグラフの言葉で言うと？

3.交友関係が連結でない場合

4.交友関係は正則グラフでないといけないらしい

4.1.定理2を利用した(II)の証明

直感的な説明

4.2.定理2の証明(1) 最小次数が1の場合

4.3.定理2の証明(2) 最小次数が2で、最大次数が2n-1の場合

4.4.定理2の証明(3) 最小次数が2n-2で、最大次数が2n-1の場合

4.4.1.次数2n-2の点が2個の場合

4.4.2.次数2n-2の点が4個以上の場合

4.5.定理2の証明(4) 最小次数が3以上2n-3以下で、最大次数が2n-1の場合

4.6.定理2の証明(5) 最小次数が2以上で、最大次数が2n-2以下の場合

4.6.1. 点Aに隣接していない点に隣接している点の次数はt

4.6.2. 点Aに隣接していない点の次数はt

4.6.3. 点Aに隣接している点の次数はt

4.6.4. 補題1の証明

5.適切な友達の人数とは？

5.1.操作後のグラフが必ず連結にならなければいけないこと

5.2.操作後が連結かつ正則グラフになる場合

6.候補の絞り込みと十分性の証明

6.1. (2n-1)-正則グラフ

6.2. n-正則グラフ

7.交友関係の言葉に戻す

3番

4番

5番

6番

8番

9番

10番

11番

16番

17番,19番,20番

18番

0.準備

1.をつくる

2.同士を掛け合わせる

3.との一致を確認する

1. $\cos \frac{\alpha +\beta }{2}, \cos \frac {\alpha -\beta }{2}$ をつくる

2. $\cos \frac{\alpha +\beta }{2}, \cos \frac {\alpha -\beta }{2}$ 同士を掛け合わせる

3. $\frac{1}{2}(\cos \alpha +\cos \beta )$ との一致を確認する