cos40°+cos80°+cos160°の値の求め方5通り

スタンダードに和積公式を用いる

2倍してから和積公式を用いる

3倍角の公式を用いる

幾何的に解く(個人的に一番好き)

2倍角の公式を用いる

2018年8月17日　少しリニューアルしました。
ちょっと質の悪い解法2つを削除して、新たに解法5を追加しました。

1. 和積公式による解法

高校数学の問題集に載っているとすればこの解法でしょう。

用いる和積公式は $\cos A + \cos B=2\cos \frac{A+B}{2} \cos \frac{A-B}{2}$ です。

$\begin{eqnarray*} \cos40^\circ+\cos80^\circ+\cos160^\circ &=& \cos40^\circ+2\cos120^\circ \cos40^\circ \\ &=& \cos40^\circ(1+2\cos120^\circ) \\ &=& 0 \end{eqnarray*}$

よって答えは $0$ となります。

2. 2倍してから和積公式を用いる解法

1つめの解法は一般的な解法ですが、こちらの方がちょっとエレガントです。

$2(\cos40^\circ+\cos80^\circ+\cos160^\circ ) \\ =(\cos40^\circ+\cos80^\circ )+(\cos80^\circ+\cos160^\circ )+(\cos40^\circ+\cos160^\circ ) \\ =2\cos20^\circ\cos60^\circ+2\cos40^\circ\cos120^\circ+2\cos60^\circ\cos100^\circ \\ =-\cos160^\circ-\cos40^\circ-\cos80^\circ \\ =-(\cos40^\circ+\cos80^\circ+\cos160^\circ)$

$2$ 倍して自身の $-1$ 倍に一致したので $\cos40^\circ+\cos80^\circ+\cos160^\circ$ は $0$ になります。

3. 3倍角の公式を用いる解法

$40^\circ ,80^\circ ,160^\circ$ という角だからこそ、この解法がハマります。
それぞれの角を $3$ 倍するとcosの値が一致するような角になるので、それを利用します。

$\begin{eqnarray*} 4\cos^3 40^\circ-3\cos40^\circ&=&\cos120^\circ=-\frac{1}{2} \\ 4\cos^3 80^\circ-3\cos80^\circ&=&\cos240^\circ=-\frac{1}{2} \\ 4\cos^3 160^\circ-3\cos160^\circ&=&\cos480^\circ=-\frac{1}{2} \\ \end{eqnarray*}$
より、 $4x^3-3x+\frac{1}{2}=0$ という方程式を考えます。
すると、 $\cos40^\circ,\cos80^\circ,\cos160^\circ$ は相異なる三数であるので、先の方程式の三解に一致します。
求めるのは三解の和なので、解と係数の関係により答えは $0$ となります。

ただのcosの和に解と係数の関係を用いるのは面白いです。副産物として $\displaystyle\cos40^\circ \cos80^\circ \cos160^\circ =-\frac{1}{8}$ も求まりました。

4. 幾何的な解法

f:id:mel9:20160911040557p:plain
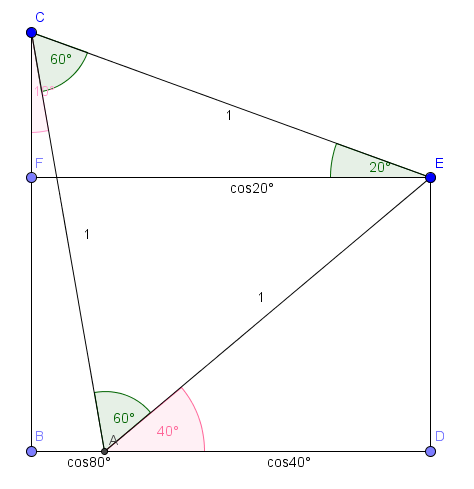
この解法がこの5つの中で最も綺麗だと思います。僕はこれが一番好きです。
3点 $\rm B,A,D$ を一直線上に並べ、 $\rm BA=\cos80^\circ,AD=\cos40^\circ$ とします。
ここで2点 $\rm C,E$ を、 $\rm \angle BAC=80^\circ, \angle DAE=40^\circ, \angle CBA=\angle EDA=90^\circ$ を満たすように、直線 $\rm BD$ に関して同じ側にとると、 $\rm AC=CE=1$ となります。
$\rm\angle CAE=60^\circ$ なので、 $\rm\triangle CAE$ は正三角形です。
よって $\rm\angle BCE=70^\circ$ なので、直線 $\rm BC$ 上の点 $\rm F$ を $\rm\angle EFC=90^\circ$ となるようにとると、 $\rm\angle CEF=20^\circ$ 。
したがって、 $\rm EF=\cos20^\circ$ となります。
$\rm EF=BA+AD$ なので、 $\cos40^\circ+\cos80^\circ-\cos20^\circ=0$ 。
すなわち、 $\cos40^\circ+\cos80^\circ+\cos160^\circ$ も $0$ です。

正三角形がうまくはまってくれるのが綺麗ですね。

5. 2倍角の公式を用いる解法

$\cos80^\circ, \cos160^\circ$ に倍角の公式を用いて $\cos40^\circ$ に帰着させます。 $\cos40^\circ$ はどうにもならないと思いきや、救世主が現れてなんとかなります。
$\begin{eqnarray*} \cos40^\circ+\cos80^\circ+\cos160^\circ &=& \cos40^\circ+2\cos^240^\circ -1+2\cos^280^\circ-1 \\ &=& \cos40^\circ+2\cos^240^\circ +2(2\cos^240^\circ -1)^2-2 \\ &=& 8\cos^440^\circ -6\cos^240^\circ +\cos40^\circ \\ &=& \cos40^\circ ( 2(4\cos^340^\circ -3\cos40^\circ ) +1) \\ &=& \cos40^\circ ( 2\cos120^\circ +1) \\ &=& 0 \end{eqnarray*}$
5つめの式から6つめの式に移るときに3倍角の公式を利用しています。

ところで、元の問題の角が $40^\circ ,80^\circ ,160^\circ$ の代わりに $80^\circ ,160^\circ ,320^\circ$ であっても、この5つめの解法の式変形はすべて行えます。 $\cos(40\times 3)^\circ = \cos(80\times 3)^\circ$ が成り立つからです。したがって、 $\cos80^\circ+\cos160^\circ+\cos320^\circ$ も $0$ になります。これは $\cos40^\circ = \cos320^\circ$ とも整合性が取れています。
ここら辺をよく考えると、 $40^\circ$ という角がうまくいく理由が見えてきて、他のきれいな式変形が可能な角を探し当てることができるかもしれませんね。